Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Electron
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's begin by discussing the charge to mass ratio of the electron. J.J. Thomson was the first to measure it in 1897. Can anyone tell me what an electron is?
It's a subatomic particle with a negative charge.
Correct! Electrons are fundamental constituents of atoms. Thomson discovered them while working with cathode ray tubes. Why do you think this was a significant discovery?
It was important because it showed that atoms are not indivisible, as previously thought.
Exactly! This finding changed the way we view atomic structure. Now, can anyone recall the actual value of the charge to mass ratio that Thomson calculated?
Was it 1.758820 Γ 10ΒΉΒΉ C/kg?
Yes! Well done. Remember this value; itβs crucial for understanding the properties of electrons.
Thomson's Experiments
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Thomson used cathode ray tubes, where electrons flow from the negative to positive electrodes. What happens when we apply electric and magnetic fields to these electrons?
They would deflect from their original path.
Exactly! The degree of deflection helps us understand the electron's charge and mass. Could someone explain how the deflection might vary?
The magnitude of deflection depends on the strength of the electric or magnetic field, the mass of the electron, and the amount of charge it carries.
Right! Thatβs how Thomson could calculate the charge-to-mass ratio. Now, based on this experimentation, do you think other subatomic particles could be measured similarly?
I think so, but it might be more complicated for particles like protons and neutrons since we cannot isolate them easily.
That's true! The principles are there, but the execution might require different techniques.
Measurement of Electron's Charge and Mass
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Following Thomson's discovery, R.A. Millikan conducted the famous oil drop experiment between 1906 and 1914. Can anyone explain what he aimed to measure?
He wanted to determine the charge of the electron, right?
Exactly! And he established the charge on the electron to be approximately -1.602176 Γ 10β»ΒΉβΉ C. How did he combine this with Thomsonβs work to find the electronβs mass?
By using the charge-to-mass ratio and the charge that Millikan found, he could calculate the mass.
Thatβs correct! This synergy between different experiments was critical in solidifying our understanding of atomic structure. What does this tell us about the importance of collaboration in scientific inquiry?
It shows that combining different research efforts can lead to greater insights and understanding!
Applications and Implications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we know the charge and mass of an electron, what implications do you think this has on our understanding of chemistry?
It probably affects how we understand chemical bonding since electrons play a huge role in forming bonds.
Spot on! The interactions of electrons define chemistry at the atomic and molecular levels. Can anyone think of a specific example where this knowledge is critical?
In ionic and covalent bonding, knowledge about electrons helps explain how atoms interact!
Thatβs right! Understanding the charge and mass leads us to predict behavior in chemical reactions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
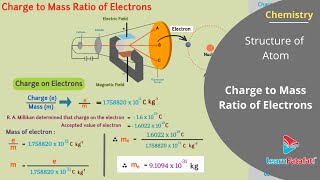
The measurement of the charge-to-mass ratio of the electron by J.J. Thomson in 1897 is a significant milestone in atomic theory. Using cathode ray tubes, Thomson demonstrated the existence of electrons and calculated their charge-to-mass ratio, which contributed to our understanding of atomic structure and the nature of subatomic particles.
Detailed
Charge to Mass Ratio of Electron
In 1897, British physicist J.J. Thomson conducted a pivotal experiment using cathode ray tubes to measure the charge-to-mass ratio (
) of electrons. By applying electric and magnetic fields, he was able to quantify how much the path of electrons deviated, leading to the determination of this ratio as
= 1.758820 Γ 10ΒΉΒΉ C/kg. This discovery established that electrons are fundamental components of all atoms, contradicting the earlier notion that atoms were indivisible.
The experiment described the behavior of electrons under electric and magnetic fields, emphasizing that their deflection depends on their charge, mass, and the strength of the fields applied. Additionally, subsequent work by Robert Millikan in the early 20th century measured the electron's charge accurately, affirming its negative charge of
= -1.602176 Γ 10β»ΒΉβΉ C, and combining this with Thomson's results to determine the mass of the electron as
= 9.1094 Γ 10β»Β³ΒΉ kg. These findings laid the foundation for modern atomic theory, paving the way for advancements in our understanding of atomic and subatomic structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Thomson's Experiment
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
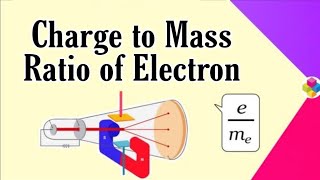
In 1897, British physicist J.J. Thomson measured the ratio of electrical charge (e) to the mass of electron (me) by using cathode ray tube and applying electrical and magnetic field perpendicular to each other as well as to the path of electrons. When only electric field is applied, the electrons deviate from their path and hit the cathode ray tube at point A. Similarly when only magnetic field is applied, electron strikes the cathode ray tube at point C. By carefully balancing the electrical and magnetic field strength, it is possible to bring back the electron to the path which is followed in the absence of electric or magnetic field and they hit the screen at point B.
Detailed Explanation
Thomson used a cathode ray tube to conduct his experiments. The cathode ray tube is a vacuum tube with two electrodesβone is the cathode (negative) and the other is the anode (positive). When electricity is passed through the tube, it creates cathode rays, which are streams of electrons. By applying electrical and magnetic fields, Thomson was able to observe how the electrons that were moving between the two electrodes deviated from their original path. By measuring where the electrons hit the screen in different field conditions (points A, B, and C), he could calculate the charge-to-mass ratio of the electron (e/me).
Examples & Analogies
Think of shooting a basketball through a hoop. If you only had wind (the electric field) blowing towards the hoop, the ball would deviate in the wind. If you had a fan (the magnetic field) blowing from the side, the ballβs path would be altered again. This is similar to how Thomson manipulated the fields to bring the electrons back onto their original path, allowing him to measure their movement accurately.
Factors Affecting Deviation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thomson argued that the amount of deviation of the particles from their path in the presence of electrical or magnetic field depends upon:
(i) The magnitude of the negative charge on the particle, greater the magnitude of the charge on the particle, greater is the interaction with the electric or magnetic field and thus greater is the deflection.
(ii) The mass of the particle β lighter the particle, greater the deflection.
(iii) The strength of the electrical or magnetic field β the deflection of electrons from its original path increases with the increase in the voltage across the electrodes, or the strength of the magnetic field.
Detailed Explanation
The deflection of electrons when influenced by an electric or a magnetic field is determined by three key factors: the charge of the electron, its mass, and the strength of the fields applied. If the charge on the electron is higher, it will experience a stronger force and deflect more. On the other hand, if the mass of the electron is lower, it will also deflect more easily. Lastly, increasing the strength of the electric or magnetic fields will increase the force acting on the electrons, causing even greater deflection.
Examples & Analogies
Imagine you're on a skateboard (the electron) being pushed in different directions by a friend (electric/magnetic field). If your friend pushes you harder (stronger field), you move more! If you're on a lighter board, you would move easier than if you were on a heavier one. Similarly, a more charged particle will move more under the same conditions.
Thomson's Findings
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By carrying out accurate measurements on the amount of deflections observed by the electrons on the electric field strength or magnetic field strength, Thomson was able to determine the value of e/me as:
e/me = 1.758820 Γ 1011 C kgβ1
Where me is the mass of the electron in kg and e is the magnitude of the charge on the electron in coulomb (C). Since electrons are negatively charged, the charge on electron is βe.
Detailed Explanation
Through meticulous experiments, J.J. Thomson calculated the charge-to-mass ratio of the electron, which gave scientists important understanding about the nature of the electron. The ratio he found was significantly large, indicating that the electron has very little mass compared to its charge. This value was groundbreaking, as it helped lay the groundwork for the study of atomic structure and the properties of subatomic particles.
Examples & Analogies
Imagine trying to find the relationship between the weight of a feather and how fast it floats through the air. Thomson's measurements were akin to figuring out that relationship for an electron, allowing scientists to understand how much 'push' (charge) it has compared to its 'weight' (mass). This insight is crucial for knowing how particles behave in different contexts.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
J.J. Thomson's measurements and discovery of the electron.
-
Charge-to-Mass Ratio and its significance.
-
Millikan's Oil Drop Experiment for measuring electron charge.
-
Calculate mass of electron using charge-to-mass ratio.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
J.J. Thomson used a cathode ray tube which demonstrated that electrons can be directed and influenced by electric and magnetic fields. By measuring the deflection of electrons, he calculated the charge to mass ratio.
-
Millikan's Oil Drop Experiment provided a method to accurately measure the charge of the electron, which further refined the understanding of atomic structure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Thomson found a charge so fine, With a mass ratio, it does align.
π Fascinating Stories
-
Once in a lab there was a beam, Of electrons that danced like a dream. Thomson was keen on what he would find, A charge-to-mass ratio was intricately designed.
π§ Other Memory Gems
-
J.J.T. β Just Jammy Thomson for measuring the electron's charge and mass relationship.
π― Super Acronyms
CEM β Charge-to-mass, and Electron Measurement!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: ChargetoMass Ratio
Definition:
The relationship between the charge of a particle and its mass, crucial for defining particle behavior in electric and magnetic fields.
-
Term: Cathode Ray Tube
Definition:
A vacuum tube containing electrons that are emitted from the cathode, used in various experiments, including those measuring electrons.
-
Term: Electric Field
Definition:
A field around charged particles that exert a force on other charges.
-
Term: Magnetic Field
Definition:
The field surrounding magnets or current-carrying wires that can affect other magnetic materials and charged particles.
-
Term: Millikan's Oil Drop Experiment
Definition:
An experiment conducted to measure the elementary electric charge of the electron.