Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding s Orbitals
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, weβll start discussing atomic orbitals, beginning with the s orbitals. Can anyone tell me what an s orbital looks like?
I think it's spherical.
Exactly! The s orbital is indeed spherical. This shape arises from the fact that the probability of finding an electron is highest at the nucleus and decreases uniformly in all directions. What can you tell me about the number of s orbitals available at each principal energy level?
There is only one s orbital for each principal energy level.
Correct! So, for example, the first energy level (n=1) has one s orbital, which we call the 1s orbital. What happens as we move to higher energy levels?
The size of the s orbital increases with higher n values.
Right again! The 2s is larger than the 1s, and the sizes keep increasing with each subsequent level. Now, let's summarize: what is the key shape of the s orbitals and how does their size change with principal quantum number?
The shape is spherical and increases in size with higher n values!
Exploring p Orbitals
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've discussed s orbitals, let's move on to p orbitals. Who can describe the shape of a p orbital?
I think p orbitals are like two lobes on either side of a plane.
That's correct! Each p orbital has two lobes, and there are three possible p orbitals per energy level starting from n=2. Can anyone name those three p orbitals?
They are 2p_x, 2p_y, and 2p_z!
Exactly! And how do these orbitals differ from the s orbitals?
The p orbitals are not spherically symmetric like s orbitals; they have distinct directional lobes.
Good observation! And what about the probability density at the node?
The probability density is zero at the nodal plane where the lobes touch.
Great! Letβs recap: p orbitals have two lobes, start from the second energy level, and have a nodal plane where the probability of finding an electron is zero. Any questions before we move on?
Introduction to d Orbitals
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs discuss d orbitals now. Can anyone describe their characteristics?
There are five d orbitals, right?
Yes! They are designated d_xy, d_xz, d_yz, d_x2-y2, and d_z2. How do you think their shapes differ from the s and p orbitals?
D orbitals are more complex, with some having cloverleaf shapes and one having a unique donut shape.
Exactly! The shapes of d orbitals arise from their mathematical descriptions. What is the starting principal quantum number for d orbitals?
They start from n = 3.
Correct! Also, d orbitals have unique nodal surfaces. Can anyone tell me the difference between radial and angular nodes?
Radial nodes are where the probability density is zero at certain distances, while angular nodes are where the probability density is zero in certain angular directions.
Well explained! To bring it all together: d orbitals have five types, start from n = 3, and are characterized by both radial and angular nodes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Understanding atomic orbitals is key to grasping electron distribution in atoms. This section outlines the shapes of the s, p, d, and f orbitals, explaining that these shapes are defined by their wave functions and how they correspond to electron probability density.
Detailed
Detailed Summary
In quantum mechanics, the shape of atomic orbitals is described by the wave function (Ο), which reveals crucial information about the probability of finding an electron in a given region of space around the nucleus. Each type of orbital corresponds to a distinct shape and electron distribution pattern:
- s Orbitals (l = 0): These orbitals are spherical in shape, with the probability of locating an electron being highest at the nucleus and decreasing uniformly in all directions. Every principal quantum level (n) has one s orbital, which increases in size as n increases.
- p Orbitals (l = 1): The three p orbitals (2p_x, 2p_y, 2p_z) each have two lobes oriented along the x, y, and z axes, separated by a nodal plane where the probability density is zero. They also increase in size and energy with increasing principal quantum number (n).
- d Orbitals (l = 2): There are five distinct d orbitals, each with complex shapes and orientations (e.g., d_xy, d_xz). These orbitals begin at n = 3 and also increase in size with higher n values, featuring both angular and radial nodes.
The boundary surface diagrams for orbitals convey these shapes only up to a specific probability (usually where the chance of locating an electron is 90%). This section emphasizes the mathematical and visual representations of these shapes, alongside their implications for the spatial distribution of electrons in multi-electron atoms.
Youtube Videos
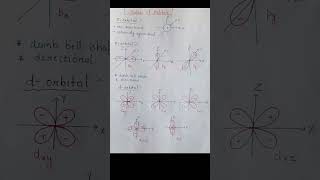
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Wave Functions and Their Meaning
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The orbital wave function or Ο for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron.
Detailed Explanation
The wave function, denoted as Ο, describes the behavior of an electron in an atom. While it provides crucial information about the electron's possible states or configurations, it does not correspond to a physical object that can be directly observed. Instead, it serves as a mathematical tool that helps us understand the probabilities of finding an electron in various locations around the nucleus.
Examples & Analogies
Think of a wave function like a weather forecast. Just as a weather report gives us a probability of rain in different areas without indicating the precise location of each raindrop, the wave function provides probabilities for where an electron might be found at any given moment, rather than pinpointing its exact position.
Boundary Surface Diagrams
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Boundary surface diagrams of constant probability density for different orbitals give a fairly good representation of the shapes of the orbitals.
Detailed Explanation
To visualize where electrons are likely to be found, scientists use boundary surface diagrams. These diagrams show the regions in space around the nucleus where there is a high probability (often set at 90%) of finding the electron. Each type of orbital has a unique shapeβs orbitals are spherical, while p orbitals are shaped like dumbbells, indicating where the probability of finding an electron is maximized.
Examples & Analogies
Imagine a swimming pool. The areas where swimmers are likely to be found are not randomly distributed; instead, they congregate in specific regions. Similar to how you might map out the busiest parts of the pool, boundary surface diagrams map out the 'busiest', or highest probability, regions surrounding the nucleus.
Shapes of s Orbitals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The boundary surface diagram for a s orbital is actually a sphere centered on the nucleus. In two dimensions, this sphere looks like a circle. It encloses a region in which probability of finding the electron is about 90%. Thus, we see that 1s and 2s orbitals are spherical in shape.
Detailed Explanation
s orbitals have a spherical symmetry, meaning the likelihood of finding an electron is uniform in all directions from the nucleus. As the principal quantum number (n) increases, such as from 1s to 2s, the size of the sphere representing the electron's probable location increases, indicating that the electron can be found farther from the nucleus while still having high probability.
Examples & Analogies
Think of a balloon. When you inflate a balloon, it becomes larger while maintaining a consistent round shape. Similarly, as we move from the 1s to the 2s orbital, the 'balloon' of probability grows larger, representing the potential positions of the electron further away from the nucleus.
Shapes of p Orbitals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In two dimensions, the boundary surface diagrams for three 2p orbitals consist of two sections called lobes that are on either side of the plane that passes through the nucleus.
Detailed Explanation
p orbitals differ from s orbitals in that they have two lobes, which represent regions where the probability density for finding an electron is high. The lobes are oriented along specific axes, such as x, y, or z, and there is a nodal plane between them where the probability density is zero. This unique shape suggests that electrons in p orbitals are more likely to be found in those lobes.
Examples & Analogies
Imagine holding a tennis ball (the nucleus) with two large pillows (the lobes of the p orbitals) on either side. The pillows represent high probability areas for finding the electron, while the area between them, where they touch, signifies a location where the electron is unlikely to be found, similar to empty space between two identical objects.
Shapes of d Orbitals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For l = 2, the orbital is known as d-orbital. There are five d orbitals with different shapes but the same energy.
Detailed Explanation
d orbitals have more complex shapes compared to s and p orbitals, with some resembling four-leaf clovers or having a more pronounced lobular structure. Each of the five d orbitals contributes to the overall space in which electrons can be found around the nucleus and all have similar energy levels, known as degeneracy.
Examples & Analogies
Think of a flower garden. Just as you might find different types of flowers (d orbitals) in the same garden bed (energy level), each with its unique shape and color, the d orbitals have distinct geometrical configurations yet exist in a similar 'energy habitat' around the nucleus.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Atomic Orbitals: Regions of space where electrons are likely found.
-
s, p, and d Orbitals: Different shapes and orientation of atomic orbitals that determine electron distribution.
-
Wave Functions: Mathematical representation of electron states.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A 1s orbital is spherical, while a 2p orbital shows two lobes that extend along different axes.
-
In a 3d orbital, there are complex shapes allowing for multi-directional electron occupancy.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Spherical like the sun, electrons hide, it's where the s orbitals bide.
π§ Other Memory Gems
-
For p orbitals, think 'lobes on display, pointing out in every way!'
π Fascinating Stories
-
Imagine a garden where s orbitals are round flowers, p orbitals are tall and pointy stalks, and d orbitals are unique clovers.
π― Super Acronyms
SPLD for Shapes
- Spherical (s)
- Pointy (p)
- Loopy (d) orbitals.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Atomic Orbital
Definition:
A region around the nucleus of an atom where the probability of finding an electron is high.
-
Term: s Orbital
Definition:
A spherical orbital where electron density is evenly distributed around the nucleus.
-
Term: p Orbital
Definition:
A bilobed orbital that has a nodal plane, existing in three orientations: p_x, p_y, and p_z.
-
Term: d Orbital
Definition:
A multi-lobed orbital with more complex shapes, existing in five forms.
-
Term: Wave Function (Ο)
Definition:
A mathematical function that describes the quantum state of a system and gives the probability distribution of an electron.