Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Viscoelastic Models
Unlock Audio Lesson
Today, we are going to explore linear viscoelastic models. These models are crucial in understanding how bituminous materials behave over time under different loads. Can anyone tell me what you think viscoelasticity means?
Does it mean the material can both stretch and flow?
Exactly! Viscoelastic materials show both elastic and viscous behavior. They can recover from deformation but also exhibit time-dependent strain. Now, let’s look at the first model: the Maxwell model. Has anyone heard of it?
Isn't that the one with the spring and dashpot?
Correct! The Maxwell model consists of a spring and dashpot in series. This means that when stress is applied, the material will deform immediately then continue to creep over time. This model helps us analyze stress relaxation, which is a key concept in pavements under load.
Maxwell Model
Unlock Audio Lesson
Can anyone summarize what the Maxwell model represents in terms of deformation?
It shows immediate deformation followed by gradual change over time, right?
Exactly! This is great for understanding how stress relaxation occurs in our materials. Now, let’s discuss the Kelvin-Voigt model. What do you think differentiates it from the Maxwell model?
The arrangement of the spring and dashpot?
Yes! In the Kelvin-Voigt model, they are arranged in parallel, which allows for some recovery of the deformation over time. This model is very useful for studying creep behavior. Can anyone provide an example of a scenario where we'd use this model?
Maybe when the pavement is settling in after construction?
Kelvin-Voigt Model
Unlock Audio Lesson
Great example! The Kelvin-Voigt model is particularly useful in scenarios involving short-term loading conditions. Now, let’s move on to the third model: Burger’s model. What does combining both models imply?
It would account for both creep and stress relaxation together?
Correct! Burger’s model combines aspects of both the Maxwell and Kelvin-Voigt models. This gives us a more comprehensive view of a material's performance under different conditions. How do you think this could benefit pavement engineers?
It helps predict pavement failure better?
Exactly! Understanding how these models work is critical for engineers to design durable pavements. To wrap up, what have we learned today about these models?
We learned how each model represents different behaviors of materials under stress over time!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers linear viscoelastic models such as Maxwell, Kelvin-Voigt, and Burger’s models, which are critical for understanding the deformative behavior of bituminous materials over time. These models help predict material responses under various loading conditions.
Detailed
Linear Viscoelastic Models
In this section, we delve into linear viscoelastic models that play a significant role in describing the complex mechanical behavior of bituminous mixes. These models—namely Maxwell, Kelvin-Voigt, and Burger’s Models—are essential for characterizing how these materials respond to stress over time under different loading conditions. Understanding these models aids engineers and researchers in predicting material performance, therefore enhancing pavement design and durability.
Key Points Covered:
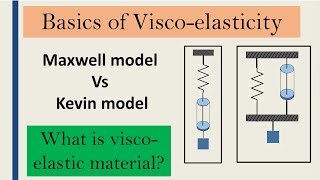
- Maxwell Model: This model depicts a combination of elastic (spring) and viscous (dashpot) elements arranged in series, representing materials that exhibit both immediate and time-dependent deformations. It is particularly useful for analyzing stress relaxation behavior.
- Kelvin-Voigt Model: Here, the spring and dashpot are arranged in parallel, illustrating materials that can recover some deformation over time, especially significant in creep behavior analysis.
- Burger’s Model: This combines elements of both the Maxwell and Kelvin-Voigt models, creating a comprehensive view of viscoelastic behavior by considering both creep and stress relaxation phenomena together.
Through these models, the analysis of creep compliance and relaxation modulus becomes fundamental, enabling better assessment and design of bituminous materials in civil engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Linear Viscoelastic Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Maxwell, Kelvin–Voigt, and Burger’s Models.
• Represent creep and relaxation behavior.
Detailed Explanation
Linear viscoelastic models are mathematical representations that describe how materials exhibit both viscous and elastic behavior when subjected to stress. The three primary linear viscoelastic models are Maxwell, Kelvin–Voigt, and Burger's models. Each model helps to understand specific aspects of material behavior, particularly under load over time.
- Maxwell Model: This model combines a spring (which represents elastic behavior) and a dashpot (which represents viscous behavior) in series. It is used to describe materials that exhibit significant flow after stress application, making it suitable for scenarios with high creep rates.
- Kelvin–Voigt Model: This model combines a spring and a dashpot in parallel. It is used to estimate materials that recover deformation over time without significant permanent deformation when stress is removed, making it particularly useful for materials that quickly regain their shape.
- Burger's Model: This model combines both the Maxwell and Kelvin–Voigt models and captures both rapid and delayed responses to stress. This model is ideal for analyzing bituminous mixes that show both immediate elastic properties and long-term viscoelastic behavior, covering a broader range of applications.
Examples & Analogies
Imagine stretching a rubber band. If you pull it quickly and let go, it snaps back into shape – illustrating the elastic component. However, if you stretch it slowly and hold, it may stay stretched and not return to its original shape as quickly, showing the viscous behavior. The Maxwell model would represent a situation where the rubber band could eventually deform permanently if held for too long, while the Kelvin–Voigt model would illustrate it quickly bouncing back. The Burger’s model effectively illustrates behavior that shows both immediate snapping back and some deformation that might last longer.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Creep: Refers to the time-dependent deformation of materials under a constant load.
-
Stress Relaxation: The reduction of stress in a material over time while maintaining a constant strain.
-
Maxwell Model: A model for materials that combines spring and dashpot behaviors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Maxwell model can be applied in predicting how asphalt will behave under prolonged heavy traffic loads during summer.
-
The Kelvin-Voigt model is exemplified by how newly laid pavement settles somewhat after compaction, allowing it to adjust slightly over time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Viscoelasticity, oh what a treat, it bends and it stretches, then comes back neat.
📖 Fascinating Stories
-
Imagine a young tree that bends in the wind (viscous) but stands straight when the storm passes (elastic). Just like the materials!
🧠 Other Memory Gems
-
Remember M-K-B: Maxwell, Kelvin-Voigt, and Burger — the three models guide our understanding.
🎯 Super Acronyms
MKB can stand for 'Models Key to Behavior' in reference to the Maxwell, Kelvin-Voigt, and Burger models.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Viscoelasticity
Definition:
The property of materials that exhibit both viscous and elastic characteristics when deformed.
-
Term: Maxwell Model
Definition:
A model featuring a spring and dashpot in series, used to represent materials that show both immediate and time-dependent deformation.
-
Term: KelvinVoigt Model
Definition:
A model where a spring and a dashpot are arranged in parallel, illustrating an ability to recover some deformation over time.
-
Term: Burger's Model
Definition:
A model that combines both the Maxwell and Kelvin-Voigt models, providing a comprehensive analysis of creep and relaxation behaviors.