Modeling Mechanical Behavior
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linear Viscoelastic Models
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore linear viscoelastic models used in bituminous mixes. Can anyone tell me what viscoelastic means?

Does it mean the material can both stretch and flow?

Exactly! Viscoelastic materials show both elastic and viscous behavior. Now, we have three main models: Maxwell, Kelvin-Voigt, and Burger’s. Who can summarize the Maxwell model?

The Maxwell model represents a material that can deform elastically and has a viscous component that allows it to flow over time.

Great summary! Let’s remember this with the acronym 'MVC' — Maxwell, Viscous, Creep. As for the Kelvin-Voigt model, does anyone know its key feature?

I think it demonstrates that deformation is recoverable, right?

Correct! So, if we summarize this section, we see how these models help us understand the time-dependent behavior of bituminous mixes.
Mechanistic-Empirical Pavement Design
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's discuss mechanistic-empirical pavement design. How do you think mechanistic models align with field data?

Are they used together to predict real-world performance?

Exactly! This combination provides a robust framework to design pavements. Can anyone give examples of distresses we model?

Fatigue cracking and rutting?

Yes! Using this approach to consider factors like traffic and temperature will enhance the durability of our designs. Remember 'M-E-P' — Mechanistic-Empirical Pavement!
Finite Element Analysis (FEA)
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s delve into Finite Element Analysis, or FEA. What do you think FEA is used for in pavement design?

To simulate how different loads affect the pavement?

Yes! FEA enables us to analyze complex interactions within pavement structures. Who can summarize the importance of using FEA?

It allows for better optimization of designs based on predicted stress and strain distributions.

Spot on! So, as a recap, today we learned about three models, the mechanistic-empirical approach, and the significance of FEA in pavement design.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section focuses on modeling the mechanical behavior of bituminous mixes through various analytical and empirical approaches, including linear viscoelastic models and finite element analysis. It emphasizes the importance of accurately predicting the performance of pavements under different loading and environmental conditions.
Detailed
Modeling Mechanical Behavior
This section outlines the models employed to understand and predict the mechanical behavior of bituminous mixes in flexible pavements. Accurate modeling is crucial for evaluating how these materials will perform under varying loads and environmental conditions.
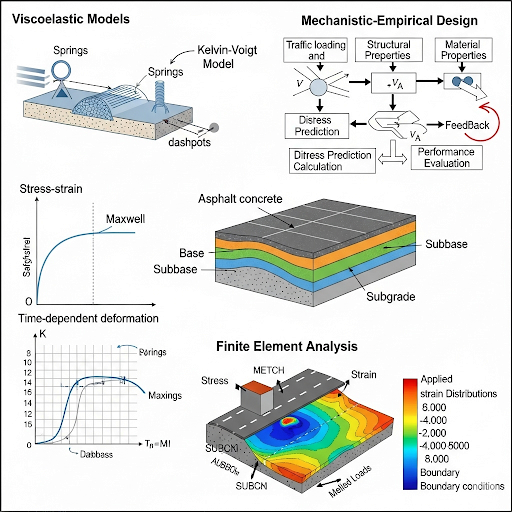
12.8.1 Linear Viscoelastic Models
The section introduces linear viscoelastic models, namely the Maxwell model, Kelvin-Voigt model, and Burger’s model, to represent the material’s creep and relaxation behavior. These models capture the time-dependent deformation characteristics that are fundamental to understanding bituminous mixes.
12.8.2 Mechanistic-Empirical Pavement Design
The mechanistic-empirical approach combines experimental data with mechanistic models to provide a comprehensive understanding of pavement performance. This hybrid method utilizes distress models related to fatigue, rutting, and thermal cracking to inform pavement design and enhance service life.
12.8.3 Finite Element Analysis (FEA)
Finite Element Analysis is highlighted as a powerful simulation tool that allows the detailed modeling of stress and strain distributions within pavement structures. FEA is particularly useful for conducting advanced research and performing optimizations when designing pavements.
12.8.1 Linear Viscoelastic Models
The section introduces linear viscoelastic models, namely the Maxwell model, Kelvin-Voigt model, and Burger’s model, to represent the material’s creep and relaxation behavior. These models capture the time-dependent deformation characteristics that are fundamental to understanding bituminous mixes.
12.8.2 Mechanistic-Empirical Pavement Design
The mechanistic-empirical approach combines experimental data with mechanistic models to provide a comprehensive understanding of pavement performance. This hybrid method utilizes distress models related to fatigue, rutting, and thermal cracking to inform pavement design and enhance service life.
12.8.3 Finite Element Analysis (FEA)
Finite Element Analysis is highlighted as a powerful simulation tool that allows the detailed modeling of stress and strain distributions within pavement structures. FEA is particularly useful for conducting advanced research and performing optimizations when designing pavements.
Understanding these models is vital for engineers to ensure that bituminous mixes are designed appropriately for their intended use, leading to roads that are safe, durable, and economical.
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Analytical and Empirical Models
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Analytical and empirical models are developed to predict the behavior of bituminous mixes under various conditions.
Detailed Explanation
This chunk introduces the idea that in order to understand how bituminous mixes behave under different conditions, researchers create both analytical and empirical models. Analytical models rely on mathematical equations to describe the behavior of materials based on physical laws. In contrast, empirical models are based on observed data from experiments and real-world scenarios. Both types of models aim to help engineers and designers make predictions about how these materials will respond during their service life, like under heavy traffic or temperature changes.
Examples & Analogies
Think of it like weather forecasting. Meteorologists use analytical models based on physics (like the movement of air and water) along with empirical models that utilize historical weather data. Together, these models help predict weather patterns, much like how bituminous mix behavior is predicted.
Linear Viscoelastic Models
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Maxwell, Kelvin–Voigt, and Burger’s Models.
• Represent creep and relaxation behavior.
Detailed Explanation
This chunk discusses specific types of linear viscoelastic models. These models are important for understanding how bituminous mixes deform over time when subjected to stress. The Maxwell model describes materials that exhibit both viscous (permanent deformation) and elastic (recoverable deformation) properties. The Kelvin-Voigt model represents materials that can deform and recover quickly. The Burger model combines both these behaviors to demonstrate more complex material responses. Understanding these models helps engineers design pavements that can withstand various stresses over their life cycle.
Examples & Analogies
Imagine a sponge that can be squeezed and then return to its original shape after the pressure is released. The sponge behaves like the elastic part of the material. However, if you keep squeezing it, the sponge eventually takes a permanent shape after a while, resembling the viscous behavior. These models help us understand when and how pavements will deform similarly.
Mechanistic-Empirical Pavement Design
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Combines mechanistic models with empirical calibration from field data.
• Uses distress models for fatigue, rutting, and thermal cracking.
Detailed Explanation
This chunk explains a design approach that merges mechanistic and empirical methods. Mechanistic models use fundamental principles of mechanics to understand material behavior, while empirical methods incorporate real-world performance data. By combining these approaches, engineers can develop designs that are more reliable and tailored to expected real-life conditions. Distress models, such as those for fatigue and rutting, allow engineers to predict when and where issues might occur, thereby improving the longevity of pavements.
Examples & Analogies
Consider a chef who wants to perfect a cake recipe. They might use scientific methods to understand how ingredients interact (mechanistic) while also adjusting based on feedback from taste tests (empirical). This combination helps them create a cake that is not only delicious but also holds its shape well, similar to how this design method enhances pavement performance.
Finite Element Analysis (FEA)
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Simulates complex stress and strain distributions in pavement structures.
• Helpful for advanced research and optimization.
Detailed Explanation
This chunk introduces Finite Element Analysis (FEA), a computational method used to analyze the behavior of bituminous mixes in pavement structures. FEA breaks down complex structures into smaller, manageable finite elements, allowing engineers to simulate how materials will behave under various loads and conditions. This technique is especially useful for advanced research, optimizing designs, and ensuring pavements can withstand predicted stresses.
Examples & Analogies
Think of building a bridge out of LEGO bricks. Each brick represents a finite element. By analyzing how each brick interacts under load, you can predict how the entire bridge will hold up when weight is applied. Similarly, FEA helps predict the performance of pavements by examining each small part of the structure.
Key Concepts
-
Linear Viscoelastic Models: Models that capture the time-dependent behaviors of bituminous mixes.
-
Maxwell Model: Represents immediate elastic response and time-dependent viscous behavior.
-
Kelvin-Voigt Model: Shows recoverable deformation under applied loads.
-
Mechanistic-Empirical Design: Combines mechanistic with empirical models to optimize pavement designs.
-
Finite Element Analysis: A powerful tool to simulate complex load interactions and stress distributions.
Examples & Applications
The application of the Maxwell model helps in predicting how asphalt behaves under varying temperature and load conditions, preventing premature road failures.
Finite Element Analysis can simulate the effects of heavy traffic loads on road pavements, allowing engineers to design more durable surfaces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Models that stretch and flow, predict how pavements grow.
Stories
Imagine an engineer assessing a pavement's health. First, they check the Maxwell model to understand its quick responses, then the Kelvin-Voigt model for recovery, and lastly, they simulate everything using FEA to ensure long-term durability.
Memory Tools
Remember 'MVK' for Maxwell, Viscous, and Kelvin—key models of behavior.
Acronyms
MEP stands for Mechanistic-Empirical Pavement design which enhances durability.
Flash Cards
Glossary
- Linear Viscoelastic Models
Models that describe how materials exhibit both viscous and elastic behavior over time.
- Maxwell Model
A linear viscoelastic model depicting material behavior with instant elastic and time-dependent viscous responses.
- KelvinVoigt Model
A model showing recoverable deformation under applied stress, combining elastic and viscous properties.
- Burger's Model
A linear viscoelastic model that combines both Maxwell and Kelvin-Voigt models to represent time-dependent behavior.
- MechanisticEmpirical Design
An approach combining mechanistic models with empirical data for pavement design and analysis.
- Finite Element Analysis (FEA)
A computational technique used to predict the behavior of structures under loads by simulating stress and strain distributions.
Reference links
Supplementary resources to enhance your learning experience.
