Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Basis
Unlock Audio Lesson
Today, we're going to talk about the concept of basis in vector spaces. Does anyone know what we mean by 'basis'?
Is it like a starting point or something?
That's a good thought! In linear algebra, a basis is actually a set of vectors that are linearly independent and can span a vector space. This means any vector in that space can be expressed as a combination of the basis vectors.
So can one vector be a basis?
Yes, if we're in a one-dimensional space, a single non-zero vector can be a basis. That's why you need to have at least as many vectors as the dimension of the space to form a basis.
What do you mean by 'linearly independent'?
Good question! Linearly independent vectors are those that cannot be expressed as a linear combination of other vectors in the set. We'll dive more into that shortly.
In summary, a basis is essential because it defines the space we are working in and helps us understand it better.
Exploring Dimension
Unlock Audio Lesson
Now, let's move on to the next concept, which is dimension. Who can tell me what dimension means in the context of vector spaces?
I think it’s about how many directions we can go in a space?
Exactly! The dimension is actually the number of vectors in the basis. For example, if you can represent your space with two vectors, then you are dealing with a two-dimensional space.
So how do we find the dimension?
To find the dimension, we just count how many vectors are in the basis. If there are three independent vectors, for instance, the dimension is three. This is crucial for understanding in civil engineering when dealing with systems modeled by vectors.
What if the vectors aren’t independent?
Great point! If the vectors are not independent, meaning some can be derived from others, they cannot all be part of the basis, and thus the actual dimension will be less than the count of those vectors.
In summary, the dimension helps us understand how vast our vector space is based on the number of independent directions we can explore.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of basis and dimension in vector spaces are explored. The basis is defined as a set of linearly independent vectors that spans the vector space, while the dimension is the number of vectors in the basis. Understanding these concepts is critical for civil engineering applications involving vector spaces and linear algebra.
Detailed
Basis and Dimension
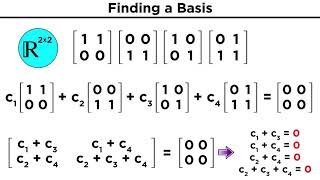
In linear algebra, basis and dimension are foundational concepts relevant to the study of vector spaces. A basis is defined as a set of vectors that are linearly independent and span the entire vector space. This means that any vector in the space can be expressed as a linear combination of the basis vectors. For example, in a two-dimensional space, two linearly independent vectors can serve as a basis.
On the other hand, dimension refers to the number of vectors in the chosen basis. It serves as a measure of the 'size' or complexity of the space. For instance:
- A vector space with a basis of two vectors is said to be two-dimensional.
- A three-dimensional space (like our physical space) has a basis of three vectors.
Understanding these concepts is vital for civil engineers because they provide the framework for dealing with problems involving systems of linear equations, transformations, and many applications across various fields of engineering.
Youtube Videos
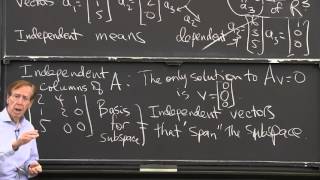
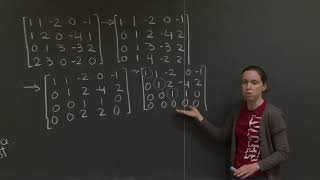
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Basis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Basis: A set of linearly independent vectors that span the space.
Detailed Explanation
In linear algebra, a basis consists of vectors that are linearly independent, meaning no vector in the set can be written as a combination of the others. These vectors also span the vector space, which means that any vector in that space can be expressed as a linear combination of the basis vectors. Essentially, a basis provides the fundamental building blocks for the entire space.
Examples & Analogies
Imagine building a house. You need a specific number of different types of building blocks (like bricks, wood, and tiles) to create the structure. Each type of block serves a different purpose but collectively, they can create any design. Similarly, basis vectors are like the essential building blocks that allow you to create every possible vector in the vector space.
Definition of Dimension
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Dimension: The number of vectors in a basis.
Detailed Explanation
The dimension of a vector space is determined by the number of vectors in its basis. For example, if a basis consists of three linearly independent vectors, then we say that the dimension of that vector space is three. This gives us important information about the structure of the space: a higher dimension indicates a more complex space, while a lower dimension indicates a simpler one.
Examples & Analogies
Think of dimension like the number of coordinates needed to locate a point in space. In a 2D space (like on a flat sheet of paper), you only need two coordinates (x, y) to specify a point. In a 3D space (like our physical world), you need three coordinates (x, y, z). Similarly, the dimension tells us how many independent vectors we need to fully describe every point in that space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Basis: A foundation set of vectors that can generate a vector space through linear combinations.
-
Dimension: A numerical measurement indicating how many vectors form a basis and define the extent of a vector space.
-
Linear Independence: A condition for vectors where none can be expressed as a combination of others in the set.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a two-dimensional plane defined by the vectors (1, 0) and (0, 1), these vectors serve as a basis and span the entire space.
-
In three-dimensional space, the vectors (1, 0, 0), (0, 1, 0), and (0, 0, 1) can form a basis and indicate that the dimension is three.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the space of points so fine, A basis holds, its vectors align.
📖 Fascinating Stories
-
Imagine a treasure map spread out on a table. The basis vectors are your compass directions, allowing you to reach every treasure marked on the map.
🧠 Other Memory Gems
-
B.A.D.: Basis, All directions covered, Dimension defined.
🎯 Super Acronyms
B.I.D.
- Basis of Independent Dimensions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Basis
Definition:
A set of linearly independent vectors that span a vector space.
-
Term: Dimension
Definition:
The number of vectors in a basis; represents the number of independent directions in a vector space.
-
Term: Linear Independence
Definition:
A condition where a vector cannot be expressed as a linear combination of other vectors in the set.