Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linear Dependence
Unlock Audio Lesson
Today we'll discuss linear dependence. A group of vectors is linearly dependent if we can express one vector as a linear combination of others. Can anyone give me an example of this?
Maybe if we have vectors like (1,2) and (2,4)?
Exactly! The second vector is just twice the first. So, we can express it as 2 * (1, 2) = (2, 4). This illustrates linear dependence.
What happens if we add another vector, say (3, 6)?
Good question! The set remains linearly dependent; the new vector can still be expressed as a combination of the first two. Thus, adding dependencies doesn't eliminate redundancy.
So, is it always just a matter of scaling?
Scaling is one way, but also consider adding or subtracting multiples. It’s important for visualizing relationships in vector spaces.
To summarize, linear dependence occurs when one vector can be formed by others in a group, which is significant in understanding redundancy in structures.
Linear Independence
Unlock Audio Lesson
Now that we understand dependence, let’s look at linear independence. A set of vectors is independent if the only combination that yields the zero vector is the trivial solution. Can anyone provide a set of vectors that are linearly independent?
What about the vectors (1,0) and (0,1)?
Excellent! They cannot be expressed as combinations of each other. So, if we set \( a_1(1,0) + a_2(0,1) = 0 \), the only solution is \( a_1 = a_2 = 0 \).
That means they span the space perfectly, right?
Correct! They form a basis for \( R^2 \). Understanding independence helps in optimizing our basis in engineering applications.
So in an engineering context, it helps to identify which constraints are necessary?
Yes! Minimizing dependence in structural models can lead to more efficient designs. Let's remember: Independence means necessity.
Practical Applications
Unlock Audio Lesson
Let's connect these concepts to civil engineering. How might we use linear dependence and independence in design?
We can analyze redundant supports in a structure!
Exactly! Recognizing which supports are redundant helps in optimizing costs and material use. Can anyone think of a case?
In bridge design, if support vectors are dependent, we could remove some without compromising stability!
Perfect! This understanding leads to effective solutions. It’s a vital step in creating reliable structures.
What if our models are too dependent and fail to consider all loading conditions?
Good point! We must ensure our models aren't overly simplistic, as that could lead to vulnerabilities. Linear independence can guide us to a more robust analysis.
So, to wrap up this session, recognizing and addressing linear dependence helps in minimizing redundancy and enhancing efficiency in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Linear dependence occurs when a combination of vectors equals the zero vector using non-zero coefficients, leading to redundancy in representation. Conversely, linear independence means only a trivial solution exists, indicating that the vectors are essential for spanning a space. This section emphasizes the relevance of these concepts in civil engineering for structural analysis and optimization.
Detailed
Linear Dependence and Independence
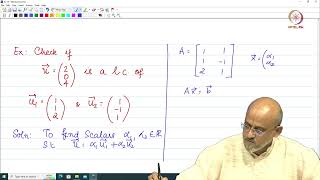
In the context of linear algebra, vectors are said to be linearly dependent if there exist scalars (not all zero) such that their linear combination results in the zero vector. Formally, for vectors \( v_1, v_2, \ldots, v_n \), they are linearly dependent if:
\[ a_1 v_1 + a_2 v_2 + \ldots + a_n v_n = 0 \]
where not all \( a_i = 0 \).
In contrast, vectors are linearly independent if the only solution to the above equation is when all coefficients are zero:
\[ a_1 = a_2 = \ldots = a_n = 0 \]
Significance in Engineering
Understanding linear dependence and independence is crucial for civil engineers, as these concepts play a significant role in analyzing structural redundancy and optimizing basis in vector spaces. This section is not just theoretical; it has practical implications in fields such as structural analysis, helping engineers create more efficient designs by identifying non-redundant, essential constraints.
Youtube Videos
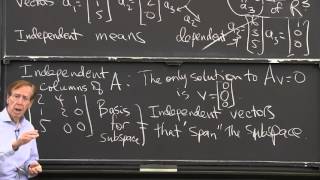
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Linear Dependence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vectors \( v_1, v_2, \ldots, v_n \) are linearly dependent if there exist scalars \( a_1, a_2, \ldots, a_n \) not all zero such that:
$$ a_1 v_1 + a_2 v_2 + \ldots + a_n v_n = 0 $$
Detailed Explanation
Linear dependence among vectors means that at least one of the vectors can be expressed as a combination of the others. In simpler terms, if you can find some coefficients (scalars) that can multiply each vector and sum them up to give the zero vector, then those vectors are dependent. The crucial part is that not all coefficients can be zero; at least one must be non-zero.
Examples & Analogies
Think of a group of friends. If one friend can be described as a combination of the others' personalities (say, they are just as funny as one friend, as smart as another, and so on), then that friend is 'dependent' on the others in terms of personality. If each friend has a unique personality that can't be duplicated by any combination of the others, they are all 'independent.'
Definition of Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vectors are independent if the only solution is when all scalars are zero:
$$ a_1 = a_2 = \ldots = a_n = 0 $$
Detailed Explanation
When vectors are linearly independent, it means that no vector can be created by combining the others. This definition emphasizes that the only way to sum these vectors and reach the zero vector is to have every scalar (the multipliers) equal to zero. In other words, every vector contributes something unique that can't be replicated by the others.
Examples & Analogies
Imagine a music band where each musician plays a different instrument. If the band can play a complete song where every musician is essential, then each musician (or vector) is independent. No musician can be fully represented by the others' contributions. If one musician stops playing, the song will be incomplete, highlighting their importance.
Application in Engineering: Structural Redundancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Linear dependence and independence are crucial for analyzing structural redundancy in engineering.
Detailed Explanation
In civil engineering, understanding whether certain forces or structural components are linearly independent helps engineers assess redundancy. For example, if multiple supports in a structure are dependent, removing one might compromise stability since they are working in concert, delivering similar contributions. Identifying independent supports can help inform design decisions for ensuring structural integrity and safety.
Examples & Analogies
Consider a bridge with several beams. If these beams are all dependent, it means that if one beam fails, the others can’t hold the structure up either. However, if each beam is independent, we know that losing one will not lead to the collapse of the bridge, as there are other beams that stand strong on their own.
Conclusion: Importance in Vector Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Understanding linear dependence and independence is fundamental for optimizing basis in vector spaces.
Detailed Explanation
The concepts of linear dependence and independence are foundational for building basis sets in vector spaces. A basis set of vectors forms a framework in which any vector in the space can be expressed. When vectors are independent, they can provide a complete set of directions in the space, which is crucial for applications in various fields, including computer graphics, physics, and engineering.
Examples & Analogies
Consider a three-dimensional space represented by the X, Y, and Z axes. To describe any point within this space, you need one direction for each axis. If any of these directions were dependent (say, one is just a combination of the others), you wouldn't have a complete way to reach every point in 3D space. Hence, the independence of these axes is vital for understanding the complete structure of three-dimensional space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Dependence: Vectors that can be defined as linear combinations of one another.
-
Linear Independence: Vectors that cannot form a linear combination that results in zero unless all coefficients are zero.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The vectors (1,2,3) and (2,4,6) are linearly dependent because one is a multiple of the other.
-
In \( R^2 \), the vectors (1,0) and (0,1) are linearly independent since they cannot be combined to represent the zero vector unless both coefficients are zero.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Dependence leads to cluttered arrays, independent lines walk clear pathways.
📖 Fascinating Stories
-
In a construction site, engineers had woods of varying lengths. Some were duplicates (dependent), while others were unique (independent) and essential for stability.
🧠 Other Memory Gems
-
Dependence shows overlap; Independence shows pure paths: D for Dependence, O for Overlap; I for Independence, P for Pure.
🎯 Super Acronyms
DI - 'D' for Dependence and 'I' for Independence; it helps remember the contrasting terms.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Dependence
Definition:
A condition where a set of vectors can be expressed as a linear combination of others, with some coefficients being non-zero.
-
Term: Linear Independence
Definition:
A situation where the only solution for a linear combination of vectors equaling the zero vector is when all coefficients are zero.