Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Diagonalization
Unlock Audio Lesson
Today, we're discussing the concept of diagonalization in matrices. A matrix is diagonalizable if it can be expressed as A = PDP⁻¹, where D is a diagonal matrix. Can anyone explain what we mean by a diagonal matrix?
A diagonal matrix has non-zero elements only on its main diagonal, right?
Exactly! Now, why might we want to diagonalize a matrix?
It makes calculations easier, especially for matrix powers!
That's right! It simplifies many operations. Remember, the eigenvalues of D are crucial in this process.
What does it mean if a matrix is not diagonalizable?
Great question! If it lacks enough linearly independent eigenvectors, it cannot be diagonalized. We'll delve deeper into that next.
Conditions for Diagonalizability
Unlock Audio Lesson
Next, let’s discuss the conditions for diagonalizability. A square matrix must have n linearly independent eigenvectors to be diagonalizable. Can anyone tell me what this means?
It means we need as many independent vectors as the dimensions of the matrix, right?
Exactly! If we have distinct eigenvalues, it guarantees we’ll have enough independent eigenvectors. What happens if some eigenvalues repeat?
We might still get linearly independent vectors if the algebraic multiplicity matches the geometric multiplicity!
Well stated! If these do not match, it signals that we may not have enough eigenvectors for diagonalization.
Importance of Diagonalization
Unlock Audio Lesson
Now that we understand the definition and conditions, let’s discuss the importance of diagonalization. One key benefit is simplifying matrix computations. Why is this helpful?
Because diagonal matrices are much easier to work with when performing operations like raising to powers!
Exactly! For example, if we want to calculate A², we can just compute D² and then combine it. Also, how is this relevant in civil engineering?
It helps with modal analysis in structures, allowing us to understand natural frequencies and vibration modes.
Right you are! Understanding these concepts is crucial for evaluating the stability of those structures.
Applications of Diagonalization
Unlock Audio Lesson
Let’s explore some practical applications. Why would civil engineers need to diagonalize matrices?
To analyze vibration modes in buildings, which helps in ensuring they can withstand stress.
Exactly! Diagonalization is also used in control systems. Anyone knows how?
It can simplify the equations governing the dynamic behavior of structures.
Perfect! Diagonalizing helps us manipulate the equations with ease. Can someone summarize the main reasons we learned about diagonalization today?
It simplifies calculations, is essential for solving differential equations, and is crucial for structural analysis.
That's a great wrap-up! Always keep these applications in mind as they are vital to your future work.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the conditions under which a square matrix can be diagonalized, emphasizing the importance of having linearly independent eigenvectors. Understanding diagonalization simplifies computations and is crucial in various applications, especially in solving systems of differential equations and structural analysis.
Detailed
Diagonalization of Matrices
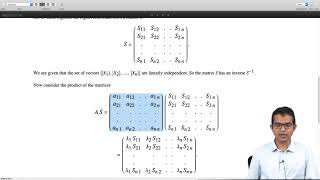
A square matrix A is said to be diagonalizable if there exists a matrix P such that:
$$ A = PDP^{-1} $$
where D is a diagonal matrix consisting of the eigenvalues of A, and P is a matrix formed from the corresponding eigenvectors. The section discusses the following key aspects:
- Conditions for Diagonalizability:
- A matrix must have n linearly independent eigenvectors (for an n x n matrix).
- If all eigenvalues are distinct, the matrix is diagonalizable.
- Importance of Diagonalization:
- It simplifies matrix computations, such as raising a matrix to a power: $$ A^k = PD^k P^{-1} $$.
- It is particularly useful in solving systems of differential equations, as diagonal matrices are easier to handle than non-diagonal ones.
- In civil engineering, diagonalization is applied in modal analysis of structures, where it aids in understanding vibration modes, which is critical for stability assessments.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A square matrix A is said to be diagonalizable if there exists a matrix P such that:
A = PDP⁻¹
where D is a diagonal matrix and P contains the eigenvectors of A.
Detailed Explanation
Diagonalization is a process that allows us to express a square matrix in a simpler form. When we say that a square matrix A is diagonalizable, it means that we can find another matrix P consisting of the eigenvectors of A and a diagonal matrix D. The equation A = PDP⁻¹ shows this relationship, where P is the matrix of eigenvectors, D is a diagonal matrix with eigenvalues on its diagonal, and P⁻¹ is the inverse of P. This simplification is beneficial in various calculations because diagonal matrices are easier to work with.
Examples & Analogies
Imagine you have a complex puzzle made of many pieces (the square matrix A). Diagonalization is like finding a way to represent that puzzle in a much simpler form (the diagonal matrix D) using a special set of reference points (the eigenvectors in matrix P). This makes it much easier to handle the puzzle, especially when you need to find solutions or piece it back together.
Conditions for Diagonalizability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Matrix must have n linearly independent eigenvectors (for an n×n matrix).
• All distinct eigenvalues imply diagonalizability.
Detailed Explanation
For a square matrix to be diagonalizable, two main conditions must be met. First, the matrix must have 'n' linearly independent eigenvectors, which means we need enough unique directions to span the space of the matrix. If we have an n×n matrix, we need exactly n eigenvectors. Second, if all the eigenvalues of the matrix are distinct, then the matrix can be diagonalized. These conditions ensure that we have the necessary structure to break down the matrix into a more manageable form.
Examples & Analogies
Think of diagonalizability like organizing a group of students based on their knowledge levels. If every student (eigenvector) has a unique capability (eigenvalue), and you can pair each student without overlap (linearly independent), you can form a perfect study group (diagonal matrix). If some students overlap in knowledge, it becomes harder to organize them effectively.
Importance of Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Simplifies matrix computations like raising a matrix to a power:
Ak = PDkP⁻¹
• Useful in solving systems of differential equations.
• Applications in modal analysis of structures (vibration modes).
Detailed Explanation
Diagonalization is important because it transforms complex matrix operations into simpler calculations. For instance, raising a diagonalizable matrix A to a power k becomes significantly easier when we use the diagonal form: Ak = PDkP⁻¹. Instead of dealing with A directly, we can manipulate the simpler diagonal matrix D. This simplification is extremely useful not only in matrix algebra but also in practical applications such as solving systems of differential equations and analyzing the vibrational behavior of structures in engineering.
Examples & Analogies
Consider diagonalization like having a complicated recipe with many steps (the original matrix). If you can break down the recipe into simpler instructions (the diagonal form), it becomes much easier to follow and replicate, such as when raising to a power. This simplification is crucial in fields such as engineering, where understanding the basic form of vibrations in a system helps in predicting how structures will behave under stress.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Diagonalization: The process of representing a matrix in a diagonal form to simplify computations.
-
Eigenvalues: The scalars that characterize how a transformation scales eigenvectors.
-
Eigenvectors: The vectors that remain in the same direction under a transformation but may be scaled by an eigenvalue.
-
Diagonal Matrix: A special case of a matrix where only the diagonal elements are non-zero.
-
Conditions for Diagonalizability: Having enough linearly independent eigenvectors is necessary for diagonalization.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider a matrix A with eigenvalues 2 and 3, then A can be expressed as A = PDP⁻¹, where D = [2, 0; 0, 3] and P contains the respective eigenvectors of A.
-
In modal analysis, diagonalization helps determine the natural frequencies of a structure, influencing design and safety assessments.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In diagonal form, values align, simplifying math, oh so fine. Eigenvectors lead the way, in D they stay, bright as day.
📖 Fascinating Stories
-
Imagine a structure needing analysis; the engineers diagonalize its stiffness matrix, finding its mode shapes through eigenvectors, ensuring stability like a well-anchored bridge.
🧠 Other Memory Gems
-
DANG! Remember: Diagonalize When All New Geometrically Independent vectors exist.
🎯 Super Acronyms
DIVA
- Diagonalization Involves Vector Analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonal Matrix
Definition:
A matrix in which all elements outside the main diagonal are zero.
-
Term: Eigenvalue
Definition:
A scalar value associated with a linear transformation that indicates how much the eigenvector is stretched or compressed.
-
Term: Eigenvector
Definition:
A non-zero vector that only changes by a scalar factor when a linear transformation is applied.
-
Term: Diagonalizable Matrix
Definition:
A square matrix that can be expressed in the form A = PDP⁻¹, where P is a matrix of eigenvectors and D is a diagonal matrix.
-
Term: Linearly Independent
Definition:
Vectors are linearly independent if no vector in the collection can be represented as a linear combination of the others.
-
Term: Characteristic Polynomial
Definition:
The polynomial obtained from the determinant of (A - λI), used to find eigenvalues.