Cayley-Hamilton Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Cayley-Hamilton Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to discuss the Cayley-Hamilton Theorem. This theorem tells us that every square matrix satisfies its own characteristic equation. Can anyone tell me what a characteristic polynomial is?

Isn't the characteristic polynomial related to the determinant of a matrix?

Exactly! The characteristic polynomial is defined as p(λ) = det(A - λI), where I is the identity matrix. So when we substitute A into this polynomial, we get p(A) = 0. Why do you think this is useful?

Maybe it can help in finding matrix inverses?

That's a great point! It can also allow us to express higher powers of A in terms of lower powers, making calculations much simpler.

So we can reduce the complexity of matrix calculations significantly?

Exactly! Let’s summarize this: The Cayley-Hamilton Theorem provides a powerful tool for manipulating and computing with matrices.
Applications of the Cayley-Hamilton Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've established what the Cayley-Hamilton Theorem states, let’s discuss a few applications. Can someone think of a specific situation where this theorem might be advantageous?

In solving systems of differential equations!

Absolutely! By using the theorem, we can express higher powers of matrices as a linear combination of smaller powers, which simplifies solving these equations dramatically. Can anyone think of another application?

What about in control systems?

Exactly! In control systems, understanding the behavior of systems often requires polynomial computations, where the Cayley-Hamilton Theorem comes into play.

This really highlights how crucial this theorem is in engineering fields!

Right! It’s used in various applications, from structural analysis to electrical engineering. Remember, the Cayley-Hamilton theorem not only simplifies theoretical calculations but also enhances practical applications.
Verifying the Cayley-Hamilton Theorem with an Example
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s verify the Cayley-Hamilton theorem with a simple matrix. Can anyone remind me how we can compute the characteristic polynomial of a matrix?

We need to find the determinant of A minus lambda times the identity matrix.

Correct! Let’s take the matrix A = [[2, 1], [1, 2]]. What would be its characteristic polynomial?

The determinant will be (2-λ)(2-λ) - 1 = λ² - 4λ + 3.

Exactly! Now, p(λ) can be written as λ² - 4λ + 3 = 0. Substituting our matrix A into this expression, we have to check if p(A) = 0. What do we get?

It leads us back to a zero matrix!

Right! This confirms the Cayley-Hamilton theorem for matrix A. Always remember that verification solidifies our understanding.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This theorem is significant in linear algebra as it allows the computation of the matrix inverse and expresses higher powers of a matrix as linear combinations of its lower powers. The characteristic polynomial of a matrix plays a pivotal role in this theorem.
Detailed
Detailed Summary
The Cayley-Hamilton Theorem is a fundamental result in linear algebra, asserting that every square matrix fulfills its characteristic equation. Given a square matrix A and its characteristic polynomial, expressed as p(λ) = det(A - λI), where I is the identity matrix, the theorem claims that substituting the matrix A into its characteristic polynomial results in the zero matrix: p(A) = 0.
Importance of the Cayley-Hamilton Theorem
The theorem is useful in various applications such as computing inverses of matrices without reverting to the adjoint method and in simplifying matrix expressions by expressing higher powers of a matrix as combinations of its lower powers. Each application emphasizes the ability to manipulate matrices in a practical and computationally efficient manner.
Youtube Videos
![Cayley-Hamilton Theorem [Control Bootcamp]](https://img.youtube.com/vi/PrfxmkBsYKE/mqdefault.jpg)




![The Cayley-Hamilton Theorem is Easy with F[x]-Modules](https://img.youtube.com/vi/1UZiI2bKO0A/mqdefault.jpg)



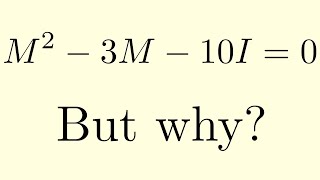
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Statement of the Theorem
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Every square matrix satisfies its own characteristic equation.
If A is a square matrix and p(λ)=det(A−λI) is its characteristic polynomial, then:
p(A)=0
Detailed Explanation
The Cayley-Hamilton Theorem states that any square matrix A will satisfy a specific polynomial equation known as its characteristic equation. The characteristic polynomial, denoted as p(λ), is calculated as the determinant of the matrix A minus λ times the identity matrix. For example, if you take a 2x2 matrix A and find its characteristic polynomial, when you substitute the matrix A into this polynomial, the result will be the zero matrix. This theorem is significant as it connects linear algebra with polynomial equations.
Examples & Analogies
Imagine a car's motion: just as the car follows a specific path based on its speed and direction, a square matrix follows a predetermined mathematical path defined by its characteristic polynomial. When we apply the car's characteristics (the matrix) into its defined rules (the polynomial), just like checking if the car returns to a stop (zero), we can predict its behavior in various conditions.
Applications of the Theorem
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Use
• To compute A−1 without adjoint method.
• To express higher powers of A as linear combinations of lower powers.
Detailed Explanation
The Cayley-Hamilton Theorem has practical applications in linear algebra. One primary use is in calculating the inverse of a matrix A without employing the adjoint method, which can be cumbersome. Instead, we can use the theorem to simplify the calculations. Additionally, it helps express higher powers of the matrix A in terms of lower powers, which is beneficial in various applications such as solving differential equations and control systems.
Examples & Analogies
Think of making a cake. Instead of adding all ingredients in one go and risking a mixture that doesn't bake well, you can follow a recipe step by step (just as we express higher powers in lower terms). The Cayley-Hamilton Theorem provides a systematic way to handle complex calculations, allowing for more manageable 'ingredients' when solving mathematical problems. Just like a good chef knows how to balance flavors and techniques, mastering this theorem equips mathematicians with powerful tools for complex scenarios.
Key Concepts
-
Cayley-Hamilton Theorem: States that every square matrix satisfies its own characteristic equation.
-
Characteristic Polynomial: Polynomial derived from the matrix to evaluate properties.
-
Matrix Substitution: The process of substituting a matrix into its characteristic polynomial to yield a zero matrix.
Examples & Applications
Using the matrix A = [[2, 1], [1, 2]], the characteristic polynomial can be found and verified through substitution.
For matrix A with a characteristic polynomial of p(λ) = λ² - 4λ + 3, substituting A in p(A) leads to the zero matrix, confirming the theorem.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Cayley and Hamilton, both said with glee, matrices solve their own polynomials, as clear as can be.
Stories
Once upon a time in Matrix-land, the wise Matrices learned that they could speak their own polynomial language, assuring them they would never be lost in calculations.
Memory Tools
Remember 'Cayley Can Pass,' for a matrix when squared, can express its power simply.
Acronyms
CHT - Cayley Hamilton Theorem, reminding you that all square matrices must obey their own characteristic equation.
Flash Cards
Glossary
- CayleyHamilton Theorem
Every square matrix satisfies its own characteristic equation.
- Characteristic Polynomial
A polynomial which is derived from the determinant of a matrix minus a scalar multiple of the identity matrix.
- Identity Matrix (I)
A square matrix in which all elements of the principal diagonal are ones and all other elements are zeros.
- Determinant
A scalar value that is a function of the entries of a square matrix, which provides important properties of the matrix.
- Matrix
A rectangular array of numbers or functions arranged in rows and columns.
Reference links
Supplementary resources to enhance your learning experience.
