Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Subspaces
Unlock Audio Lesson
Today we're talking about subspaces. A subspace is essentially a subset of a vector space that retains the properties of a vector space under the operations of addition and scalar multiplication. Can anyone tell me why understanding subspaces is essential?
I think it's because they help simplify problems by breaking them down into smaller, manageable parts.
Exactly! And could someone remind the class what properties a set of vectors needs to meet to be considered a subspace?
It needs to be closed under addition, closed under scalar multiplication, and must include the zero vector.
Correct! Remember the acronym **CAS**: C for closure under addition, A for inclusion of the zero vector, and S for closure under scalar multiplication.
What does it mean to span a space?
Good question! Spanning a space means that any vector in that space can be expressed as a linear combination of the vectors in the basis of the subspace.
So the basis is important for understanding the 'shape' of the subspace?
Exactly right! To recap: A subspace must satisfy the closure properties and contain the zero vector. Understanding these points is vital for any applications we might encounter.
Basis and Dimension of a Subspace
Unlock Audio Lesson
Now let's dive a bit deeper into the concepts of basis and dimension. What do we mean by the basis of a subspace?
The basis is a set of linearly independent vectors that can span the subspace.
Exactly! And how about the dimension? Does anyone remember how we define it?
The dimension is the number of vectors in the basis for that subspace.
Correct! So, for example, if we had a basis of 3 vectors, we would say that the dimension of that subspace is 3. The dimension tells us how many degrees of freedom we have. Can anyone think of practical applications for subspaces?
In engineering maybe? Like when analyzing forces in different structures?
Or in computer graphics to define dimensions of objects!
Great examples! Understanding basis and dimension is critical in applications ranging from engineering to visual computations. In summary, a basis is a linearly independent set spanning the subspace, and dimension reflects the number of basis vectors you have.
Applications of Subspaces in Engineering
Unlock Audio Lesson
Let’s discuss how subspaces apply in civil engineering. Why do you think understanding subspaces is crucial in this field?
Because structures can be modeled as vector spaces, and analyzing them requires understanding their properties.
Exactly! In structural analysis, we can represent different forces acting on a structure using vectors, which can help in simplifying the computations needed to ensure stability.
Also, models of fluid flow can be represented as subspaces!
Yes! And by understanding the dimensionality of those flow models, engineers can better predict behavior under different conditions. So remember, subspaces help us simplify and model complex systems effectively. To wrap up, subspaces allow for a deeper understanding of dimensionality in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
A subspace is defined as a subset of a vector space that meets the criteria to be considered a vector space itself, including closure under addition and scalar multiplication. Key concepts include basis and dimension, which describe how a subspace can be spanned by a set of linearly independent vectors.
Detailed
Subspace
A subspace is a significant concept in the context of vector spaces. It can be thought of as a smaller vector space contained within a larger one, possessing the same algebraic structure. For a subset of vectors to qualify as a subspace, it must fulfill specific conditions related to vector addition and scalar multiplication. These conditions include closure under addition and multiplication by scalars, containing the zero vector, and satisfying the necessary properties (such as associativity and distributivity) inherent to vector spaces.
Additionally, the notions of basis and dimension are important within subspaces:
The basis refers to a set of linearly independent vectors that span the subspace.
The dimension is defined as the number of vectors in this basis set. Understanding subspaces is essential for comprehending more complex structures in linear algebra, and they play a crucial role in various applications, particularly in engineering disciplines.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Subspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A subset of a vector space that is itself a vector space under the same operations.
Detailed Explanation
A subspace is essentially a smaller vector space that fits within a larger vector space. For a collection of vectors to be considered a subspace, it must satisfy specific criteria: it must be closed under addition and scalar multiplication. This means that if you take any two vectors in the subspace and add them together, and if you take any vector in the subspace and multiply it by a scalar, the results must also remain in the subspace.
Examples & Analogies
Imagine a classroom as a vector space, containing all students (vectors). If we consider a specific group of students, like those studying mathematics, that group is a subspace. Even if those students work together on math problems (addition) or study alone (scalar multiplication), they remain within that group.
Basis and Dimension
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Basis: A set of linearly independent vectors that span the space.
• Dimension: The number of vectors in a basis.
Detailed Explanation
The concept of a basis is crucial in understanding vector spaces and subspaces. A basis is formed by a set of vectors that are linearly independent, meaning no vector in the set can be written as a combination of the others. This set of vectors must also span the space, meaning that any vector in the subspace can be expressed as a combination of the basis vectors. The dimension of a subspace tells us how many vectors are needed to form a basis for that space, providing a measure of its 'size'.
Examples & Analogies
Think of a simple bicycle ride. The set of directions (north, east, south, west) that can be taken to reach your friend’s house is akin to a basis in a two-dimensional space. Each direction (vector) contributes uniquely to getting you there. The total number of directions you can take to reach any point from your starting point in this flat surface (the dimension) tells you how many distinct methods you have available to navigate.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Subspace: A subset of a vector space that is itself a vector space.
-
Basis: A set of vectors in a subspace that are linearly independent and span the space.
-
Dimension: The number of vectors in a basis for the subspace.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
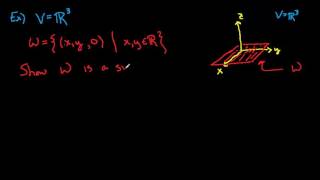
The set of all vectors in R² forms a subspace of R³, since the zero vector is included, and it is closed under addition and scalar multiplication.
-
Consider the vectors { (1, 2), (3, 4) } in R². They span a subspace in R², and if they derive from a basis, they define the dimensions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A subspace exists in vector land, with closure and structure, it takes a stand.
📖 Fascinating Stories
-
Imagine a kingdom where smaller towns represent subspaces, each with its own village leadership, akin to bases that govern dimensions within the kingdom.
🧠 Other Memory Gems
-
Remember CBZ for a subspace: Closure, Basis, Zero vector.
🎯 Super Acronyms
Use **BDS** to remember
- Basis
- Dimension
- Subspace.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Subspace
Definition:
A subset of a vector space that is also a vector space under the same operations.
-
Term: Basis
Definition:
A set of linearly independent vectors that span a vector space or subspace.
-
Term: Dimension
Definition:
The number of vectors in a basis, indicating the number of degrees of freedom in the subspace.