Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Rank
Unlock Audio Lesson
Today, we'll learn about the rank of a matrix. Can anyone tell me what they think the rank signifies in terms of the rows or columns of a matrix?
Is it about how many rows or columns are needed to describe the matrix?
Exactly! The rank of a matrix is the maximum number of linearly independent row or column vectors. So, it tells us how many dimensions the matrix spans. We can think of it as the 'weight' of the matrix's information.
So, if all rows are dependent, will the rank be zero?
Great question! Yes, if all rows or columns are dependent, the rank will be zero. Remember, rank indicates the number of independent vectors.
Methods to Find Rank
Unlock Audio Lesson
Now that we understand what the rank is, let's discuss how we can find it. What methods do you think we can use?
Maybe row-reduction like Gaussian elimination?
Absolutely! Row-reduction is one effective method. You can also convert a matrix to its echelon form and count the non-zero rows. This will give you the rank. Can anyone think of why that might be useful?
Is it because it helps us in solving systems of equations?
Yes! The rank helps us determine the consistency of systems. If the rank equals the number of variables, we can decide on the existence of solutions.
Applications of Rank
Unlock Audio Lesson
Can anyone share where you think knowing the rank of a matrix could be applied in civil engineering or real life?
Maybe in determining if structures are stable?
Exactly! Understanding the rank can help analyze stresses and stability in structures. It's fundamental in ensuring safety in engineering designs.
Does it also help with other vector space concepts?
Yes! The rank is crucial for determining the dimension of vector spaces, influencing many areas in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The rank of a matrix is defined as the maximum number of linearly independent row or column vectors. Key methods to find the rank include echelon form and row-reduction techniques. Understanding rank is crucial for determining the consistency of systems of equations and analyzing vector spaces.
Detailed
Rank of a Matrix
The rank of a matrix is a fundamental concept in linear algebra, defined as the maximum number of linearly independent row or column vectors within the matrix. This concept is vital in multiple areas, including solving systems of linear equations and understanding the dimensionality of vector spaces.
Methods to Find Rank
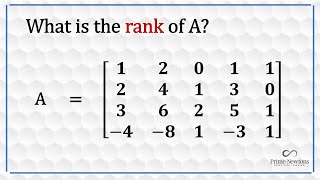
- Echelon Form: The rank can be determined by converting the matrix into its echelon form, where the rank corresponds to the count of non-zero rows in this form.
- Row-reduction: Utilizing elementary row operations to bring the matrix to a specific form can also effectively help in determining the rank.
Applications
- The rank of a matrix is useful in determining the consistency of linear systems, where the rank of the coefficient matrix informs if there are no, one, or infinitely many solutions.
- Additionally, it helps in understanding the dimension of vector spaces, providing insight into the relationships and structure of vector quantities.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The rank of a matrix is the maximum number of linearly independent row or column vectors.
Detailed Explanation
The rank of a matrix gives us a way to measure how much information the matrix contains. Specifically, it tells us how many vectors in the matrix do not depend on one another. If we can express one vector as a combination of others, it means that vector does not add any new information, and thus isn't counted in the matrix's rank. Therefore, the rank is determined by finding the maximum set of vectors that can stand alone without forming combinations with one another.
Examples & Analogies
Imagine a classroom with students where each student represents a vector in a matrix. If some students can totally solve a problem using answers from other students, their contributions are like dependent vectors — we don't count them separately as they don’t bring new solutions. The maximum number of students who can present completely independent solutions is like the rank of the classroom.
Methods to Find Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Echelon form: Count of non-zero rows.
• Row-reduction using elementary row operations.
Detailed Explanation
To determine the rank of a matrix, one effective method is to convert it into a simpler form known as echelon form. In this form, the leading entry of each non-zero row (known as the pivot) appears to the right of the pivot in the previous row. Once in this form, we can simply count the number of non-zero rows, which directly tells us the rank. Another method involves performing row operations to simplify the matrix until it reveals its rank through the arrangement of non-zero rows.
Examples & Analogies
Think of organizing a messy room to find out how many unique items you have. First, you could line things up (like row-reduced form), and then you count items (non-zero rows) to see how many distinct pieces you own. This process helps you figure out how many different categories of things you really have, similar to finding the rank of a matrix.
Applications of Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Determining the consistency of systems.
• Understanding the dimension of vector spaces.
Detailed Explanation
The rank of a matrix has significant applications in linear algebra, primarily in assessing the consistency of systems of equations. If the rank of the coefficient matrix equals the rank of the augmented matrix, the system has at least one solution and is consistent. Additionally, the rank can help us understand the dimension of vector spaces; for instance, if you have a vector space spanned by a set of vectors, the rank indicates how many dimensions this space fills.
Examples & Analogies
Imagine you have a garden with a variety of plants. The rank is like knowing how many distinct types of plants you have. If every type can grow independently without overlapping, you’re maximizing the use of space (dimension of the vector). If some plants share the same type or function, they may not add new dimensions and could be considered redundant, much like dependent vectors in a system of equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Maximum number of independent vectors: The rank represents how many linearly independent row or column vectors exist in a matrix.
-
Echelon form method: A standard method of determining rank by converting to echelon form and counting non-zero rows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A matrix with three rows and two independent rows has a rank of 2, indicating it can span a 2-dimensional space.
-
The rank of a square matrix can indicate its invertibility; if the rank equals the number of rows, it is invertible.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Rank defines the space we can span, independent rows, that’s the plan.
📖 Fascinating Stories
-
Imagine a musician. Each note represents a vector. If the notes are repeated, they lose their independence, just like non-independent rows in a matrix. The rank can be thought of as the unique melody created from those notes.
🧠 Other Memory Gems
-
RANK: 'Really Awesome Number of Keys' - to remember that it's an amazing number showing independence.
🎯 Super Acronyms
R.I.V.E.R
- Rank Indicates Vector's Essential Relationships.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rank
Definition:
The maximum number of linearly independent row or column vectors in a matrix.
-
Term: Echelon Form
Definition:
A form of a matrix where all non-zero rows are above any rows of all zero values, facilitating the identification of rank.