Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Systems of Linear Equations
Unlock Audio Lesson
Today we will start with systems of linear equations. Can anyone tell me what a system of linear equations is?
It's a combination of equations that relate the same set of variables.
Exactly! And in what forms can these systems be presented?
We can write them in general form or matrix form.
Correct! The matrix form is particularly useful for larger systems. Now, who can explain why we need consistency in systems?
It's important because it tells us if there is at least one solution, right?
Exactly! Here's a tip: think of consistency as the keyword 'existence.' Now, let's summarize: systems can be consistent or inconsistent based on the existence of solutions. Good! What are some methods to solve these systems?
We can use substitution or elimination, and for larger systems, matrix methods like Gauss elimination.
Well done! Remember to think of Gauss as your go-to for larger systems! Let's quickly recap: Systems of linear equations can be represented in different forms, and we can analyze their consistency using various solution methods.
Matrices and Their Operations
Unlock Audio Lesson
Next, let’s dive into matrices. What is a matrix?
It's a rectangular array of numbers arranged in rows and columns.
Perfect! Now, who can list some types of matrices?
Row matrix, column matrix, zero matrix, diagonal matrix, and identity matrix.
Great job! The identity matrix is particularly important. Can anyone explain what it does?
It acts like 1 in multiplication for matrices.
Exactly! It’s our '1' of matrices. Now, let's talk about matrix operations. What can we do with matrices?
We can add, subtract, and multiply them.
That's right! Remember, matrix addition and subtraction require dimensions to match. A helpful acronym is **A**dd and **S**ubtract: **A**ll **S**ame size. Now, let’s summarize: Matrices are crucial in various forms and have unique properties that guide our operations.
Eigenvalues and Eigenvectors
Unlock Audio Lesson
Let’s now explore eigenvalues and eigenvectors. Who can give me a definition?
Eigenvalues are scalars that show how much a vector is stretched or squished during a transformation.
Good! And what about eigenvectors?
They are the vectors that change only by the scalar factor during a transformation.
Exactly! Eigenvalues give us crucial information about a matrix’s behavior. Now, how do we find them?
By solving the characteristic equation!
Correct! And remember, the characteristic equation is derived from the determinant of A minus lambda times I, set to zero. To help remember this method, just recall: **D**eterminant **A**fter **L**ambda, and you'll always know how to tackle it! Now let's recap: Eigenvalues give us insight into a matrix's behavior, and we find them using the characteristic equation.
Applications in Civil Engineering
Unlock Audio Lesson
Finally, let’s discuss applications in civil engineering. How does linear algebra come into play?
In structural analysis to solve for forces and displacements.
Exactly! We can use linear algebra to ensure structures can withstand loads. Can someone tell me an application in geotechnical engineering?
Modeling soil behavior, right?
Right again! Now, how about in water resource engineering?
We can analyze flow distribution networks using matrix equations.
Perfect! A quick tip to remember: **F**ix **S**tructures, **G**uarantee **W**ater flow, and you'll recall the major applications! To wrap up: Linear algebra is a critical tool in various engineering fields, aiding in structural integrity and resource management.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section on Linear Algebra in civil engineering covers systems of linear equations, matrix types, operations, inverse matrices, eigenvalues, and their applications in engineering. It emphasizes methods for solving complex problems faced by civil engineers using linear algebra techniques.
Detailed
Linear Algebra
Linear Algebra serves as the foundation for various applied mathematics domains, significantly in civil engineering. This section addresses critical topics such as:
- Systems of Linear Equations: A foundational concept where we analyze sets of linear equations through various solution methods, including substitution, elimination, and matrix methods.
- Matrices and Operations: Detailing matrix constructs, types (like row, column, and identity matrices), and essential operations like addition, multiplication, and finding inverses.
- Eigenvalues and Eigenvectors: Critical for understanding structural stability and other engineering phenomena, they arise from solving characteristic equations and provide insights into system behaviors.
- Applications in Civil Engineering: Linear algebra plays a crucial role in evaluating structural integrity, modeling fluid dynamics, and forming accurate simulations in transportation and geotechnical fields.
- Advanced Concepts: Additional discussion on the diagonalization of matrices, the Cayley-Hamilton theorem, and numerical solutions that form essential tools in the engineer's toolkit. The exploration of vector spaces, orthogonality, and minimal polynomials rounds out this exploration.
Understanding these foundational elements underlines the importance of linear algebra in real-world engineering problems, particularly those involving extensive system analyses.
Youtube Videos
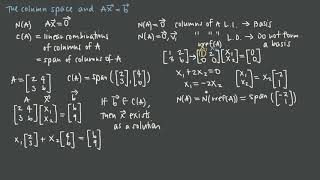
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Algebra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Linear Algebra is the cornerstone of modern mathematics and has extensive applications in Civil Engineering. It plays a crucial role in the analysis of structures, solving systems of linear equations, transformations, optimization, and numerical simulations. Engineers often encounter real-world problems that can be modeled using matrices and vectors — whether it's analyzing forces in a truss, planning construction logistics, or simulating fluid flow. This chapter covers the fundamental concepts of linear algebra with the level of detail required for aspiring civil engineers.
Detailed Explanation
Linear Algebra is a branch of mathematics that deals with vectors and matrices. It is essential for solving problems in various fields, especially civil engineering. In structural analysis, for instance, engineers use linear algebra to understand how forces distribute through structures. Also, linear algebra helps in transforming data and optimizing designs in engineering projects.
Examples & Analogies
Think of linear algebra as a toolkit for engineers. Just like a carpenter needs different tools to build a house, engineers need linear algebra concepts to analyze and design structures effectively. For example, when building a bridge, engineers use linear equations to ensure it can bear the weight of cars and withstand winds.
Systems of Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A system of linear equations is a collection of one or more linear equations involving the same set of variables.
Forms
- General Form (2 variables):
$$a_1x + b_1y = c_1 \ a_2x + b_2y = c_2$$ - Matrix Form:
$$AX = B$$
where A is the coefficient matrix, X is the variable matrix, B is the constant matrix.
Detailed Explanation
A system of linear equations consists of equations that represent relationships between variables. For example, in the general form with two variables (x and y), you can visualize each equation as a line on a graph. The point(s) where these lines intersect represent the solutions to the system. In matrix form, the equations are compactly represented as a multiplication of matrices.
Examples & Analogies
Imagine you're at a store and buying apples and oranges. If you know you have $4 to spend, and apples cost $1 each while oranges cost $2 each, you can set up equations for your purchases (like how many of each you can buy). By solving these equations systems, you can figure out how many of each fruit you can buy.
Solution Methods for Systems of Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solution Methods
- Graphical Method (only practical for 2 or 3 variables)
- Substitution and Elimination
- Matrix Methods (preferred for large systems):
– Gauss Elimination
– Gauss-Jordan Elimination
– LU Decomposition
– Matrix Inversion Method
Detailed Explanation
Different methods exist for solving systems of linear equations depending on their complexity and size. For smaller systems, the graphical method can be useful where you plot equations on a graph. For more complex systems, especially with many variables, matrix methods like Gauss elimination break down the equations step-by-step to find solutions systematically.
Examples & Analogies
Think about cooking a meal that requires multiple ingredients. If you need 2 cups of flour, 1 cup of sugar, and 3 eggs, you can adjust your recipe easily by substituting or eliminating some ingredients based on what you have. In a similar way, when solving linear equations, you alter the equations to isolate unknowns, just like adjusting your recipe to fit what’s available in your kitchen.
Types of Systems - Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consistency of a System
- Consistent: At least one solution exists.
- Inconsistent: No solution exists.
- Infinitely many solutions: When the rank of the augmented matrix equals the number of variables and the system is dependent.
Detailed Explanation
Systems of linear equations can be consistent or inconsistent. A consistent system means it has solutions, which could be one specific solution or infinitely many. In contrast, an inconsistent system has no solution, indicating something about the equations contradicts each other. Understanding this consistency helps engineers evaluate whether their models can produce valid outcomes.
Examples & Analogies
Imagine trying to plan a meeting where everyone has different times available. If everyone can agree on a time, that's a consistent situation—the meeting can happen! But if one person can only meet at a time when others can’t, that's inconsistent—there's no way to have the meeting at the same time. Similarly, systems of equations must balance to be solvable.
Types of Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Types of Matrices
- Row Matrix: 1 row only.
- Column Matrix: 1 column only.
- Zero or Null Matrix: All elements are zero.
- Diagonal Matrix: Non-zero elements only on the principal diagonal.
- Scalar Matrix: Diagonal matrix with equal diagonal elements.
- Identity Matrix (I): Diagonal matrix with all diagonal elements as 1.
- Symmetric Matrix: A=AT
- Skew-Symmetric Matrix: A=−AT
- Upper/Lower Triangular Matrix: All elements below/above the diagonal are zero.
- Singular Matrix: Determinant is 0.
- Non-Singular Matrix: Determinant is not 0.
Detailed Explanation
Matrices come in various types, each serving different purposes in linear algebra. For instance, a diagonal matrix has non-zero entries only on its diagonal, which simplifies calculations. An identity matrix acts like the number 1 in multiplication for matrices, as multiplying any matrix by the identity matrix leaves it unchanged. Recognizing these types helps in selecting appropriate methods for solving engineering problems.
Examples & Analogies
Think of matrices like boxes that hold different shapes. Just as some boxes can only hold cubes (diagonal matrices) while others can hold multiple shapes (general matrices), different types of matrices serve special functions in computations, making it easier to solve various engineering problems, like calculating forces on different parts of a structure.
Matrix Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Matrix Operations
- Addition and Subtraction:
- Possible only for matrices of the same dimension.
- Performed element-wise.
- Scalar Multiplication:
- Multiply every element of the matrix by a scalar.
- Matrix Multiplication:
- Not commutative: AB ≠ BA
- Defined if the number of columns in A equals the number of rows in B.
Detailed Explanation
Matrix operations include addition, scalar multiplication, and matrix multiplication. In addition, only matrices of the same size can be added together element by element. Scalar multiplication involves multiplying every element of a matrix by a number. Matrix multiplication is different; it combines rows and columns in a specific manner and does not follow commutativity, meaning the order in which you multiply matrices matters.
Examples & Analogies
Imagine adding two grocery lists (matrices) that have the same number of items. You can simplify them by combining their contents (addition). However, if you try to combine them in a way that doesn’t match (like multiplying different lists), you’ll end up with a mess—this represents the operations being specific in how they must be performed!
Determinants and Their Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Determinants
- A scalar value associated with square matrices.
- Important for invertibility and system solutions.
Properties
- det(AB)=det(A)det(B)
- det(AT)=det(A)
- If det(A)=0, then A is singular and non-invertible.
Detailed Explanation
The determinant is a crucial number that can tell us about a square matrix's properties. It helps determine if a matrix is invertible—if it's zero, you can't switch it back (invert). The properties of determinants, like how the determinant of a product equals the product of determinants, help in simplifying calculations and understanding behaviors in complex systems.
Examples & Analogies
Think of a determinant as a key that helps you unlock the functionality of a matrix. If the key (determinant) turns out to be faulty (zero), you can’t use that door (matrix). When evaluating engineering problems, knowing whether you have the right keys (invertible matrices) ensures that you can successfully navigate through complex calculations.
Inverse of a Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Definition
If A is a square matrix, its inverse A−1 exists such that:
$$AA^{-1} = A^{-1}A = I$$
Conditions
- Only non-singular matrices have an inverse.
Methods to Find Inverse
- Adjoint Method:
$$A^{-1} = \frac{adj(A)}{det(A)}$$ - Gauss-Jordan Method
Detailed Explanation
The inverse of a matrix is like reversing a function; when you multiply a matrix by its inverse, you get the identity matrix. However, only non-singular matrices (those with a non-zero determinant) have inverses. The adjoint method is one way to find an inverse, while the Gauss-Jordan method systematically uses row operations to find it.
Examples & Analogies
Consider a recipe where you first add ingredients and then 'invert' by taking them out in a precise way to return to your initial state. Similarly, the inverse matrix helps you go back to the original state, showing how you can manipulate equations to find unknowns in engineering calculations.
Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
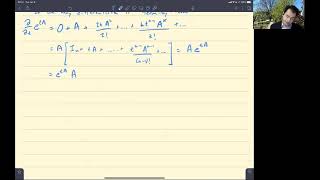
Definition
For a square matrix A, a non-zero vector v and scalar λ such that:
$$Av = λv$$
Here, λ is called the eigenvalue and v is the eigenvector.
Finding Eigenvalues
- Solve the characteristic equation:
$$det(A−λI)=0$$
Finding Eigenvectors
- Solve:
$$(A−λI)v = 0$$
Detailed Explanation
Eigenvalues and eigenvectors are fundamental in linear algebra, especially in applications like stability analysis. An eigenvector points in a direction that remains invariant under the transformation applied by a matrix, with the eigenvalue indicating how much it stretches or contracts in that direction. Finding them involves calculating the determinant to set up equations that help reveal these properties.
Examples & Analogies
Imagine pushing a long, flexible rod in the water. The direction the rod bends represents the eigenvector, while the amount it bends is like the eigenvalue. Understanding how structures respond under forces is critical for engineers to ensure stability and safety in constructions.
Applications of Linear Algebra in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications of Linear Algebra in Civil Engineering
- Structural Analysis: Solving equilibrium equations, deflection, and force distribution.
- Transportation Engineering: Traffic flow and optimization models.
- Geotechnical Engineering: Stability analysis and soil behavior modeling.
- Water Resource Engineering: Flow distribution networks.
- Computer-Aided Design (CAD): Transformations, rotations, and projections of objects.
- Finite Element Method (FEM): Uses matrices to approximate solutions in structural systems.
Detailed Explanation
Linear algebra plays a critical role in various engineering fields. For instance, engineers use it in structural analysis to ensure buildings can support weight and resist forces. In transportation, linear models help optimize traffic flow to reduce congestion. The Finite Element Method (FEM) uses matrix techniques to solve complex problems, aiding in simulations of real-world situations.
Examples & Analogies
Think of linear algebra as the blueprint for engineering solutions. Just as architects need blueprints to create buildings, engineers use the principles of linear algebra to create models for bridges, roads, and other structures. It’s all about turning complex problems into manageable equations that lead to safe and effective designs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Systems of Linear Equations: A collection of linear equations involving the same set of variables that can be solved using various methods.
-
Matrix: An array of numbers organized into rows and columns utilized for various mathematical calculations.
-
Eigenvalues and Eigenvectors: They represent important properties of a matrix showcasing the directional behavior under transformations.
-
Applications in Civil Engineering: Linear algebra principles are applied in analyzing structures, simulations, and modeling real-world systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a linear equation system can include equations such as 2x + 3y = 6 and 4x - y = 5, which can be solved using substitution or elimination methods.
-
A real-world application might involve calculating forces in a truss system using matrices to derive solutions efficiently.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Matrices can multiply, add and more, solve equations, open the door.
📖 Fascinating Stories
-
Imagine a kingdom where numbers live in rows and columns, finding their place to fight equations and share tales of their transformations.
🧠 Other Memory Gems
-
For matrix operations, just remember Multiplication, Add, Subtract: M.A.S. for quick calculations!
🎯 Super Acronyms
To recall eigenvalues
- **E**igenvectors **I**ndicate **D**irection
- hence **E.I.D.** for key insights.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Equation
Definition:
An equation that represents a straight line when graphed, involving variables raised to the first power.
-
Term: Matrix
Definition:
A rectangular arrangement of numbers in rows and columns used to represent and solve systems of equations.
-
Term: Eigenvalue
Definition:
A scalar value indicating how much a corresponding eigenvector is stretched or squished during a linear transformation.
-
Term: Eigenvector
Definition:
A non-zero vector whose direction remains unchanged when a linear transformation is applied.
-
Term: Rank of a Matrix
Definition:
The maximum number of linearly independent column or row vectors in a matrix.
-
Term: Consistency
Definition:
A property of a system of equations indicating whether at least one solution exists.
-
Term: Inverse Matrix
Definition:
A matrix that, when multiplied by the original matrix, results in the identity matrix.