Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Consistent and Inconsistent Systems
Unlock Audio Lesson
Welcome everyone! Today, we're diving into the consistency of a system of linear equations. Can anyone tell me what a consistent system is?
Is it when there’s at least one solution?
Exactly! A consistent system means there is at least one solution. Now, what about an inconsistent system?
It means there are no solutions, right?
Yes! An inconsistent system cannot be solved. To remember this, think of 'inconsistent' as 'in-no-solution'. Can anyone think of a situation where these might apply?
Maybe in structural analyses, some systems end up being impossible to satisfy?
Great point! In real-world applications, such as engineering, understanding these terms is vital.
Let’s summarize what we’ve learned about consistent and inconsistent systems.
Infinitely Many Solutions
Unlock Audio Lesson
Now, let's talk about systems that have infinitely many solutions. What do we need for that to occur?
Is it when the rank of the augmented matrix equals the number of variables?
Absolutely correct! When the rank of the augmented matrix is equal to the number of variables, it indicates that the equations are dependent. Why is this such a critical point to recognize?
Because it shows how many different ways we can satisfy the equations?
Exactly! Infinite solutions provide flexibility in design and modeling. For instance, civil engineers sometimes deal with forces and balances that can be achieved in numerous ways.
Let's recap our discussion on solutions within linear systems.
Application in Engineering
Unlock Audio Lesson
How do you think understanding system consistency applies to civil engineering models, like structural analysis?
It helps ensure that structures can support weight without failing!
Correct! Engineers must solve for conditions that keep their structures safe based on consistent systems of equations.
So, knowing whether a system is consistent directly impacts the feasibility of a design?
Exactly! If a system turns out inconsistent, then engineers will need a different approach. Let’s review what we’ve connected between consistency and engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains the concept of the consistency of a system of linear equations, outlining three scenarios: consistent systems with at least one solution, inconsistent systems with no solutions, and systems with infinitely many solutions. It emphasizes the importance of these conditions for understanding linear equations in engineering applications.
Detailed
Consistency of a System
In linear algebra, a system of linear equations is deemed consistent if at least one solution exists. Conversely, a system is inconsistent if no solutions can be found. Furthermore, some systems can have infinitely many solutions, which occurs when the rank of the augmented matrix equals the number of variables, representing dependent equations. Understanding these definitions is crucial for solving practical engineering problems, enabling civil engineers to model various scenarios accurately.
Youtube Videos
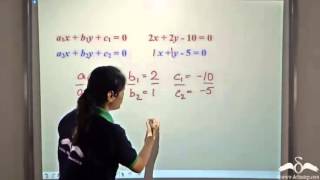
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Consistent: At least one solution exists.
• Inconsistent: No solution exists.
Detailed Explanation
In linear algebra, we classify systems of equations based on their solutions. A 'consistent' system is one that has at least one solution; this means you can find at least one set of values for the variables that satisfy all the equations simultaneously. An 'inconsistent' system, on the other hand, has no solution at all, indicating that the equations contradict each other and cannot be true at the same time.
Examples & Analogies
Imagine a scenario where two friends are trying to meet at a specific location at the same time. If one friend is at point A and the other is at point B, and they both claim they have to get to point C at exactly the same time, this could be consistent if they both can reach point C together or it could be inconsistent if their paths do not allow it.
Types of Consistency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Infinitely many solutions: When the rank of the augmented matrix equals the number of variables and the system is dependent.
Detailed Explanation
A system of equations can also have infinitely many solutions, which occurs when the equations are dependent on each other. In such cases, the rank of the augmented matrix (which includes the constants) is the same as the number of variables in the system. This means that instead of having a single solution, there are multiple combinations of variable values that satisfy all equations. Thus, there is a whole 'line' or 'plane' of solutions.
Examples & Analogies
Think of a situation where you have a recipe for a fruit punch. If the recipe allows for various amounts of different juices that can mix together to create the same flavor, you can have multiple ways to achieve that final taste. Similarly, in this case, the many combinations of juices correspond to the infinitely many solutions of our system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Consistency: Determines if a solution exists for a system of equations.
-
Inconsistency: Indicates that no solution can satisfy the equations.
-
Infinite Solutions: Occurs when equations are dependent and provide numerous solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of consistent system: A system with equations x + y = 2 and x - y = 0 has a unique solution (x=1, y=1).
-
Example of inconsistent system: A system with equations x + y = 2 and x + y = 4 has no solution.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To solve a line and find your way, a consistent system is here to stay; no solutions bring inconsistency, look for overlap to find the key.
📖 Fascinating Stories
-
Imagine two roads on a map; one was lost and can't meet, representing an inconsistent system — a dead-end street. The other was clear with paths intertwining, showing a consistent system with a common finding.
🧠 Other Memory Gems
-
C-I-I: Consistent in Inconsistent, Infinite in Intersection.
🎯 Super Acronyms
C for Consistent (solution exists), I for Inconsistent (no solution), and I for Infinite (countless solutions).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Consistent System
Definition:
A system of linear equations that has at least one solution.
-
Term: Inconsistent System
Definition:
A system of linear equations that has no solution.
-
Term: Infinite Solutions
Definition:
A situation where a system of equations has countless solutions, often due to dependent equations.