Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Basics of Matrix Multiplication
Unlock Audio Lesson
Today, we will explore matrix multiplication, a crucial operation in linear algebra. Let’s start with an important rule: Matrix multiplication is not commutative, meaning that AB is not the same as BA. Can anyone explain why that might be important?
It's important because in some applications, the order might change the results, like in solving systems of equations.
Exactly! Now, does anyone know the requirements for multiplying two matrices?
You need the number of columns in the first matrix to equal the number of rows in the second matrix.
Correct! If A is an m × n matrix and B is an n × p matrix, what would be the size of the resulting matrix C = AB?
It would be m × p!
Great job! Each element of C can be found by taking the dot product of the corresponding row from A and the corresponding column from B. Let's summarize: Matrix multiplication is not commutative, requires compatible dimensions, and results in a new matrix. Now let's move on to some examples.
Calculating Elements in Matrix Multiplication
Unlock Audio Lesson
Let's dive deeper into how we calculate each element in a matrix product. For instance, if we have A which is a 2x3 matrix and B which is a 3x2 matrix, how would we find the first element of the resulting matrix?
We take the first row of A and the first column of B and calculate the dot product.
Exactly! If A = [[1, 2, 3], [4, 5, 6]] and B = [[7, 8], [9, 10], [11, 12]], can anyone calculate the first element of the resulting product matrix C?
Yeah, it would be 1*7 + 2*9 + 3*11, which equals 58.
Correct! Now, if we continue this method for all elements, we can construct the entire matrix product. Remember, practice is key to mastering this. We will work on some exercises next.
Applications of Matrix Multiplication
Unlock Audio Lesson
Now that we've tackled the theory and calculations, let's discuss where matrix multiplication is used in real life. Can anyone think of significant applications?
It's used in computer graphics when transforming images.
It’s also important in systems of linear equations used in engineering!
Great examples! In fact, civil engineers use matrices to model structural loads and analyze forces within structures. Remember, understanding matrix multiplication is crucial for problem-solving in engineering. Let’s summarize: Matrix multiplication is used broadly across various fields, emphasizing its importance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the rules and properties of matrix multiplication, highlighting its non-commutative nature and the conditions required for the operation. Matrix multiplication is crucial in various applications in engineering and mathematics, making it a foundational skill for students.
Detailed
Matrix Multiplication
Matrix multiplication is an operation that combines two matrices into a new matrix. It is widely used in linear algebra for various applications, including solving systems of linear equations, performing linear transformations, and in numerous engineering problems.
Key Points:
- Non-Commutative: Matrix multiplication is not commutative, which means that for two matrices A and B, AB is not necessarily equal to BA.
- Dimension Requirement: The multiplication of two matrices is defined only when the number of columns in the first matrix A equals the number of rows in the second matrix B. If A is of size m × n and B is of size n × p, the resulting matrix C will be of size m × p.
- Element Calculation: Each element of the resulting matrix C is computed as the dot product of the corresponding row from matrix A and the corresponding column from matrix B.
- Applications: Matrix multiplication is utilized across various disciplines for tasks such as transformations in computer graphics, solving equations in engineering, and statistical analysis in data science. It serves as a powerful tool for modeling and solving real-world problems in civil engineering.
Youtube Videos
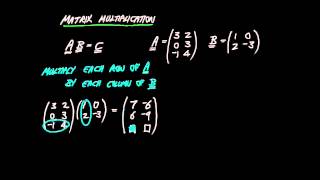
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Matrix Multiplication Defined
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Matrix Multiplication
• Not commutative: AB ≠ BA
• Defined if the number of columns in A equals the number of rows in B.
Detailed Explanation
Matrix multiplication involves combining two matrices to produce a third matrix. The key condition for multiplying two matrices is that the number of columns in the first matrix (let's call it A) must be equal to the number of rows in the second matrix (call it B). This permits the elements of A to be paired with the elements of B in a specific way to yield a new matrix. It’s important to note that matrix multiplication is not commutative. This means that the order in which you multiply the matrices matters; AB is not necessarily the same as BA.
Examples & Analogies
Think of matrix multiplication like combining a recipe with a batch of cookies where the order matters. If you mix ingredients in one order, you get a certain type of cookie, but if you switch the order, you could end up with something entirely different or not even recognizable as a cookie.
Conditions for Matrix Multiplication
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Defined if the number of columns in A equals the number of rows in B.
Detailed Explanation
For two matrices to be multiplied, it is crucial first to check their dimensions. If matrix A has dimensions m × n (m rows and n columns) and matrix B has dimensions p × q, multiplication can only take place if n = p. When this condition is satisfied, the resulting product matrix C will have dimensions m × q. This means the resultant matrix’s number of rows will equal the number of rows in matrix A and the number of columns will equal the number of columns in matrix B.
Examples & Analogies
Imagine you are making a smoothie (matrix A), and you can only add fruits (matrix B) if you have the right quantity of each fruit measured out in a specific bowl (dimensions matching). If your bowl size (row/column) does not match the amount of fruit you want to incorporate from your recipe, you can’t make that smoothie.
Non-commutativity of Matrix Multiplication
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Not commutative: AB ≠ BA.
Detailed Explanation
Non-commutativity in matrix multiplication means that switching the order of multiplication will generally lead to different results. For example, if A is a 2x3 matrix and B is a 3x2 matrix, you can multiply A by B (resulting in a 2x2 matrix), but you cannot multiply B by A without performing a different operation—this will lead to undefined dimensions for the product. Hence, understanding that AB and BA can give entirely different matrices is fundamental for working with multiple linear systems.
Examples & Analogies
Consider doing a group project where order matters. If one group member creates an outline (matrix A) and another one adds details (matrix B), the outline followed by details (AB) is structured differently than adding details first without an outline (BA), which may lead to confusion or a less coherent project.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Matrix Multiplication: Fundamental operation combining two matrices.
-
Non-Commutative Property: The order of multiplication matters.
-
Dimension Compatibility: Number of columns in the first matrix must equal the number of rows in the second.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given A = [[1, 2], [3, 4]] and B = [[5, 6], [7, 8]], the product AB = [[19, 22], [43, 50]].
-
To calculate the element C[1][2], take the dot product of Row 1 of A and Column 2 of B: (16 + 28) = 22.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Matrix A and B, when multiplied,
📖 Fascinating Stories
-
Imagine rows in a dance, matching columns' chance,
🧠 Other Memory Gems
-
D.C.M: Dimensions must match for the columns and rows.
🎯 Super Acronyms
N.C.D
- Not Commutative
- Dimensions must align.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Matrix Multiplication
Definition:
An operation that takes two matrices and produces a new matrix, defined only when the number of columns in the first matrix equals the number of rows in the second matrix.
-
Term: NonCommutative
Definition:
A property indicating that the order in which two matrices are multiplied affects the result, meaning AB ≠ BA.
-
Term: Dot Product
Definition:
A calculation that involves multiplying corresponding entries of two sequences of numbers and summing those products.