Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Algebra's Role in Civil Engineering
Unlock Audio Lesson
Today, we're exploring the foundational role of Linear Algebra in Civil Engineering. Can anyone tell me how Linear Algebra is beneficial in this field?
It helps in analyzing structures and ensuring they can withstand loads.
Exactly! By using matrices, we can model complex systems. Now, can anyone explain what a sparse linear system is?
I think it's when there are many zeros in a matrix, making it easier to solve.
Great point! Sparse matrices reduce computational effort. Remember, we focus not just on solutions but on stability and behavior predictions.
Eigenvalues and Structural Dynamics
Unlock Audio Lesson
Now, let’s dive into eigenvalues. Why do you think they are critical in structural analysis?
They help predict the natural frequencies of structures, which can indicate how they will respond to forces.
Exactly! Eigenvalues are key to identifying stability issues. Can anyone explain how this relates to the real-world application in engineering?
In earthquakes, determining the eigenvalues can help us design buildings to better withstand seismic forces.
Precisely! This is why understanding linear algebra is critical for civil engineers. It’s not just theory; it has direct applications in safety.
Matrix Decomposition Techniques
Unlock Audio Lesson
Let’s talk about matrix decomposition. Who can give a brief overview of what it is?
It breaks down matrices into simpler forms which makes calculations easier.
Absolutely! It simplifies solving systems of equations. How does this relate to our engineering simulations?
It allows for quicker computations which is necessary in simulations, especially when testing various scenarios.
Great points! Remember, efficient calculations lead to timely and accurate results in structural design processes.
Conclusion and Real-world Applications
Unlock Audio Lesson
To wrap up, how can we summarize the role of Linear Algebra in civil engineering?
It helps in modeling, analyzing, and solving complex structural systems.
And it enhances our ability to predict how structures will behave under different loads!
Exactly! With this understanding, you all are better prepared to tackle engineering challenges and optimize designs. Keep these concepts in mind as they are crucial for your future work.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The role of Linear Algebra in Civil Engineering encompasses various applications, from optimizing structural design through matrix methods to ensuring the stability of complex systems via linear transformations. Understanding these concepts is essential for effectively tackling engineering challenges.
Detailed
Role of Linear Algebra in Civil Engineering
Linear Algebra serves as a fundamental tool in Civil Engineering, enabling engineers to model and solve complex problems. It provides the framework needed for analyzing structures, where various factors must be considered to ensure stability and functionality. Key areas of application include:
- Creating and Solving Large Sparse Linear Systems: Engineers often work with large datasets that describe physical systems. Linear Algebra simplifies the representation and manipulation of these systems using matrices, making it easier to find solutions for engineering problems.
- Eigenvalue Problems in Dynamic Analysis: Eigenvalues derived from matrices are essential to understand system dynamics, applicable in seismic analysis and stability checks.
- Matrix Decomposition Techniques: These methods enhance the accuracy and efficiency of numerical simulations, essential in predicting structural behavior under load.
Engineers are equipped to tackle real-world challenges with these mathematical tools, employing them in various scenarios from transportation modeling to hydrodynamic studies.
Youtube Videos
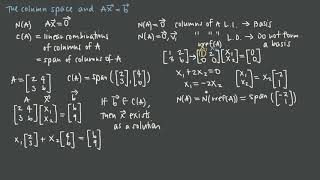
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Context of Finite Element Method (FEM)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
FEM is used for approximating solutions in complex geometries. Matrix equations such as [K]{u}={F} are formed, where:
– K = Stiffness Matrix,
– u = Displacement Vector,
– F = Force Vector.
Detailed Explanation
In the context of Finite Element Method (FEM), engineers use mathematical models to approximate solutions for complex structures and geometries. The representation of these structures involves the formation of matrix equations. The equation [K]{u}={F} consists of three main components:
1. K (Stiffness Matrix): This matrix represents the stiffness properties of the structure. It contains coefficients that relate the displacements of nodes to the forces acting on them.
2. u (Displacement Vector): This vector indicates the displacement of each node in the structure. It describes how much each point in the material moves when subjected to forces.
3. F (Force Vector): This vector contains the external forces applied to the structure.
Together, these elements help in solving for unknown displacements when forces are known, allowing engineers to analyze structural behaviors.
Examples & Analogies
Imagine you're building a bridge over a river. Instead of analyzing the entire bridge at once, you can break it down into smaller sections, or 'elements.' Each element can be analyzed using a basic model (like a spring), where the stiffness matrix 'K' tells you how much it will stretch or compress under loads. By understanding how each part behaves, you can predict how the entire bridge 'u' will move under heavy traffic 'F'.
Application of Linear Algebra in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Role of Linear Algebra
• Constructing and solving large sparse linear systems.
• Eigenvalue problems in dynamic analysis.
• Matrix decomposition for stability and accuracy.
Detailed Explanation
Linear algebra serves multiple crucial roles in engineering, particularly in the FEM context:
1. Constructing and Solving Large Sparse Linear Systems: Many engineering problems result in large matrices with a lot of zero entries, which are known as sparse matrices. Linear algebra techniques allow engineers to efficiently solve these systems, reducing computational time.
2. Eigenvalue Problems in Dynamic Analysis: Eigenvalues and eigenvectors help engineers understand the dynamic behavior of structures, such as determining vibrational modes and natural frequencies, which are critical for ensuring stability and safety.
3. Matrix Decomposition for Stability and Accuracy: Methods like LU decomposition allow the breaking down of matrices into simpler components to enhance the stability and accuracy of solutions, making calculations more reliable and manageable.
Examples & Analogies
Think of cleaning a cluttered room. Instead of addressing everything at once, you can break it down into manageable sections. In engineering, linear algebra does just that by breaking down complex challenges into simpler linear equations that can be solved quickly. For example, understanding the vibrational modes of a building helps engineers design it to withstand earthquakes, ensuring safety just like organizing your room helps you find your favorite book more quickly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Algebra: Essential for modeling and solving engineering problems.
-
Sparse Linear Systems: Facilitate efficient computation in complex systems.
-
Eigenvalues: Critical for predicting structural responses to dynamic loads.
-
Matrix Decomposition: Enhances computational efficiency in numerical simulations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using eigenvalue analysis to assess vibrations in a bridge structure.
-
Applying matrix decomposition to simplify calculations in finite element modeling.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In structures great and small, matrices help us all. Sparse and deep, they show us how to keep our projects neat and sound.
📖 Fascinating Stories
-
Once in a town, engineers faced a daunting challenge to build a bridge. They used linear algebra to explore its stability, ensuring it stood strong against storms and quakes.
🧠 Other Memory Gems
-
EIEO - Eigenvalues Indicate Energy Output, reminding us their role in dynamic analysis.
🎯 Super Acronyms
FEMS - Finite Element Method Simplified
- Remember the role of linear algebra in FEM and simulations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Algebra
Definition:
A branch of mathematics dealing with vector spaces and linear mappings between these spaces.
-
Term: Matrix
Definition:
A rectangular array of numbers arranged in rows and columns.
-
Term: Sparse Matrix
Definition:
A matrix predominantly filled with zeros, often leading to techniques that exploit this sparsity for more efficient computing.
-
Term: Eigenvalue
Definition:
A scalar associated with a linear transformation, indicating the factors by which the eigenvector is scaled.
-
Term: Decomposition
Definition:
The process of breaking down a matrix into simpler, constituent parts to facilitate easier computation.