Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Minimal Polynomial
Unlock Audio Lesson
Today, let's discuss the minimal polynomial of a matrix. The minimal polynomial is defined as the monic polynomial of the least degree such that m(A) = 0. Can anyone tell me what this means?
Does it mean that when you plug the matrix into the polynomial, it gives you the zero matrix?
Exactly! Great answer. This polynomial effectively captures the essence of the matrix's behavior when applied to vector spaces.
So, why is it important to have the smallest degree?
The least degree ensures that we can identify the simplest polynomial that characterizes the matrix. Higher-degree polynomials might introduce unnecessary complexity.
What does 'monic' mean?
Good question! A monic polynomial is one where the leading coefficient is 1.
Can the minimal polynomial tell us if the matrix is diagonalizable?
Absolutely! If the minimal polynomial has distinct linear factors, the matrix is diagonalizable.
To summarize, the minimal polynomial is crucial for understanding a matrix's structural properties and for applications in control systems.
Relation to Characteristic Polynomial
Unlock Audio Lesson
Now, let's examine how the minimal polynomial is related to the characteristic polynomial. Can anyone remind me what a characteristic polynomial is?
I think it’s the determinant of (A - λI) set to zero, right?
Exactly! The characteristic polynomial is derived from the matrix in this way. The minimal polynomial always divides the characteristic polynomial. Why do you think that relationship is important?
Maybe it shows that any roots of the minimal polynomial are also roots of the characteristic polynomial?
Correct! This indicates a shared structure between the two polynomials. The roots of the minimal polynomial give us insight into the eigenvalues derived from the characteristic polynomial.
So if the characteristic polynomial has repeated roots, does that mean the minimal polynomial does too?
Yes, but the minimal polynomial will capture the least multiplicity necessary to annihilate the matrix.
In conclusion, understanding the relationship between these two polynomials is vital for matrix analysis and applications.
Applications of Minimal Polynomial
Unlock Audio Lesson
Let's talk about some practical applications of the minimal polynomial. Can anyone give an example of where this concept might be used in civil engineering?
Maybe in structural behavior analysis?
That's correct! In structural engineering, it helps in modeling dynamic behaviors of structures.
What do you mean by dynamic behavior?
Dynamic behavior refers to how structures respond to forces over time, like vibrations. The minimal polynomial provides insight into these responses.
And in control systems too, right?
Exactly! In control systems, the minimal polynomial helps determine the stability and controllability of systems modeled by matrices. It plays a crucial role!
To recap, the minimal polynomial is essential not just in analysis but also in the practical design and engineering of systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The minimal polynomial serves to characterize a matrix by providing the smallest polynomial that, when applied to the matrix, yields the zero matrix. It plays a significant role in understanding properties like diagonalizability and relates directly to the characteristic polynomial.
Detailed
Minimal Polynomial
The minimal polynomial of a matrix A is defined as the monic polynomial m(x) of the least degree such that :
$$ m(A) = 0 $$
This polynomial uniquely characterizes the action of the matrix on the vector space and provides insights into its structure. Notably, the minimal polynomial always divides the characteristic polynomial of the matrix, establishing a fundamental relationship between these two important polynomials.
Key Points:
- The degree of the minimal polynomial indicates the size of the largest Jordan block associated with the matrix, which displays critical information about the algebraic and geometric multiplicities of its eigenvalues.
- Understanding the minimal polynomial is crucial for determining if a matrix is diagonalizable; specifically, if the minimal polynomial has distinct linear factors, the matrix can be diagonalized.
- Applications of the minimal polynomial are prominent in areas such as control systems and structural behavior analysis.
In summary, the minimal polynomial is not only pivotal in theoretical aspects of matrix algebra but also in practical scenarios encountered in engineering.
Youtube Videos
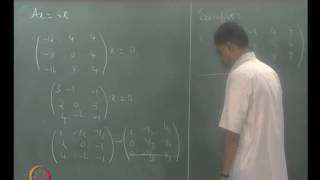
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Minimal Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The minimal polynomial of a matrix A is the monic polynomial m(x) of least degree such that:
m(A)=0
Detailed Explanation
The minimal polynomial, denoted as m(x), is a specific polynomial associated with a matrix A. The term 'monic' means that the leading coefficient (the coefficient of the highest degree term) is 1. The polynomial m(x) is the simplest polynomial that, when the matrix is substituted into it (i.e., evaluating m(A)), results in the zero matrix. This indicates that the polynomial captures all the essential behavior of the matrix in terms of linear transformations.
Examples & Analogies
Imagine you are tuning a musical instrument. The minimal polynomial is like the specific note that perfectly resonates, causing the instrument to produce a clear sound. Just as finding that one note is critical to tuning the instrument, identifying the minimal polynomial helps us understand the character of a matrix.
Relation to Characteristic Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Always divides the characteristic polynomial.
• Degree of minimal polynomial gives the size of the largest Jordan block.
Detailed Explanation
The characteristic polynomial is another important polynomial associated with a matrix, often used to determine eigenvalues. The essential point here is that the minimal polynomial of matrix A will always divide its characteristic polynomial. This means you can think of the minimal polynomial as a simplified version that provides critical insights into the structure of the matrix. Additionally, the degree of the minimal polynomial indicates the size of the largest Jordan block in the Jordan form of the matrix, which relates to how the eigenvalues behave and their algebraic multiplicity.
Examples & Analogies
Think of the characteristic polynomial as a full recipe for a complex dish. The minimal polynomial is like a simplified version of that recipe that captures the essential flavors—enough to impress without all the extra details. Understanding both helps in achieving the best results when working with the matrix.
Applications of Minimal Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Helps in determining diagonalizability.
• Essential in control systems and structural behavior analysis.
Detailed Explanation
The minimal polynomial has several important applications in linear algebra. First, it aids in determining whether a matrix can be diagonalized. A matrix can be diagonalized if its minimal polynomial can be factored into linear terms. Additionally, in control systems, the minimal polynomial is used to assess stability, while in structural behavior analysis, it helps in understanding how systems will respond to different loads and stresses.
Examples & Analogies
Consider a bridge that must withstand varying loads. Engineers use the minimal polynomial to predict how the structure will react under stress, ensuring the bridge is stable and safe over its lifespan. It's as if the minimal polynomial is a blueprint, allowing engineers to foresee any potential issues before they arise.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Minimal Polynomial: The shortest monic polynomial that annihilates a matrix.
-
Characteristic Polynomial: A polynomial used to find the eigenvalues of a matrix.
-
Diagonalizability: The property of a matrix that allows it to be represented as diagonal.
-
Jordan Block: Associated with the minimal polynomial, indicating the structure of a matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A with minimal polynomial m(x) = (x-1)(x-2), it can be concluded that A is diagonalizable since the roots are distinct.
-
If the minimal polynomial of a matrix has a repeated root, eigenvectors must be examined for their independence.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When a matrix's roots are clear, minimal polynomial is here!
📖 Fascinating Stories
-
Imagine a matrix lost among the various polynomials. The minimal polynomial finds it, showing the simplest path through the polynomial forest!
🧠 Other Memory Gems
-
M.A.R.C. - Minimal Affects Relationship Characterization: Remember how minimal polynomials characterize matrices.
🎯 Super Acronyms
M.P. - Monic Polynomial
- It is simple to remember because it must have a leading coefficient of 1!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Minimal Polynomial
Definition:
The monic polynomial of least degree such that m(A) = 0 for matrix A.
-
Term: Characteristic Polynomial
Definition:
The polynomial obtained as the determinant of A - λI, used to determine eigenvalues.
-
Term: Monic Polynomial
Definition:
A polynomial where the leading coefficient is 1.
-
Term: Jordan Block
Definition:
A block matrix used to represent linear transformations with eigenvalues.
-
Term: Diagonalizable Matrix
Definition:
A matrix that can be represented in a diagonal form through a similarity transformation.