Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues and Eigenvectors
Unlock Audio Lesson
Today we'll begin discussing eigenvalues and eigenvectors, two very important concepts in linear algebra. Can anyone tell me why they think these concepts are significant?
I think they’re crucial for understanding how matrices transform space, right?
Yeah, and I heard they also help in analyzing structures in engineering!
Exactly! Eigenvalues and eigenvectors come into play in various applications such as structural stability. Now, let’s define them clearly. An eigenvalue is a scalar obtained from the characteristic equation, and the corresponding eigenvector is a non-zero vector that satisfies the equation Av = λv. We'll explore how to find these vectors in our next session.
Finding Eigenvalues
Unlock Audio Lesson
To find eigenvectors, we first need eigenvalues. Can anyone remind us how we find eigenvalues?
We solve the characteristic equation, which is det(A−λI)=0.
Right! And that gives us the possible values for λ.
Perfect! Once we have those λ values, we can substitute them back into our system. Next, let's write the equation (A−λI)v = 0, and explore how we can solve it for v. This is how we find our eigenvectors.
Finding Eigenvectors
Unlock Audio Lesson
Alright, let’s delve into the process of finding eigenvectors. After finding an eigenvalue λ, we set up the equation (A−λI)v = 0. What does this form look like in practice?
We end up with a homogeneous system of linear equations!
I think we can find multiple solutions based on that matrix system.
That's right! Depending on the multiplicity of the eigenvalue, there can be one or more linearly independent eigenvectors. It’s important to recognize that scaling an eigenvector doesn’t change its status as an eigenvector. Let’s discuss a specific example next.
Applications of Eigenvectors
Unlock Audio Lesson
We've learned how to find eigenvectors. Now, can anyone share where we might use these in civil engineering?
They’re used in modal analysis to understand the natural frequencies of structures.
And in stability analysis to check if structures will hold under certain conditions!
Exactly! Eigenvectors help us analyze not just the behavior of structures but also the principal stresses and the material properties. Understanding these applications solidifies the importance of our findings. Great work today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the process of finding eigenvectors, which involves solving the linear equation
(A−λI)v = 0, where A is the matrix, λ is the eigenvalue, and v is the eigenvector. The significance of eigenvectors extends to practical applications in fields like structural engineering and stability analysis.
Detailed
Finding Eigenvectors
In the study of linear algebra, eigenvectors are vital components that arise when dealing with square matrices. These vectors allow us to understand transformations represented by the matrix. Given a square matrix A, an eigenvector v is defined such that:
$$Av = λv$$
where λ is the corresponding eigenvalue. To find eigenvectors, once we have determined the eigenvalues by solving the characteristic polynomial (det(A−λI)=0), we need to substitute each eigenvalue back into the equation:
$$(A−λI)v = 0$$
This equation is a homogeneous system of linear equations. The solution v will give us the eigenvector(s) associated with the eigenvalue λ.
In practical applications, finding eigenvectors is crucial. In fields such as civil engineering, it aids in modal analysis of structures, determining stability, and analyzing principal stresses and strains. Thus, the ability to find eigenvectors is not only fundamental in theoretical mathematics but also essential in applied sciences where structural integrity and optimization are emphasized.
Youtube Videos
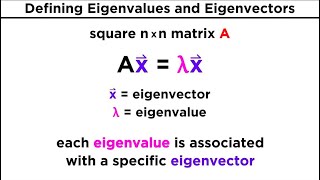
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a square matrix A, a non-zero vector v and scalar λ such that:
Av = λv
Here, λ is called the eigenvalue and v is the eigenvector.
Detailed Explanation
In this definition, consider a square matrix 'A' that represents transformations in space. An eigenvector 'v' is a special vector that, when transformed by matrix 'A', does not change its direction; it only gets scaled by the eigenvalue 'λ'. Therefore, the product of the matrix and the vector results in a vector that is a multiple of the original vector, which encapsulates the concept of invariance under that transformation.
Examples & Analogies
Think of it like a spinning top that stays upright while spinning. The top can change where it's pointing when you give it a push (the matrix transformation), but its upright orientation (the eigenvector) remains unchanged as long as it’s spinning smoothly.
Finding Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Solve the characteristic equation:
det(A−λI)=0
Detailed Explanation
To find the eigenvalues of the matrix A, we first formulate the characteristic equation, which is achieved by determining the determinant of the matrix (A - λI) equal to zero. Here, 'I' represents the identity matrix of the same size as 'A', and λ stands for the eigenvalue we're looking for. The solutions to this equation will give us the eigenvalues of the matrix.
Examples & Analogies
Imagine you're trying to find the heights of various trees in a forest where each tree can stretch to a different height based on certain conditions (like weather). By setting up a system where you measure factors affecting the trees (the matrix A) and find the specific conditions that lead to certain tree heights (the eigenvalues), you can isolate which conditions lead to which tree heights.
Finding Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Solve:
(A−λI)v = 0
Detailed Explanation
Once we have the eigenvalues λ, the next step is to find the corresponding eigenvectors. This is done by substituting the eigenvalue back into the equation (A - λI)v = 0. This equation states that the vector 'v' should satisfy the system of equations resulting from that operation. We typically need to solve this system using methods for solving linear equations, yielding one or more eigenvectors associated with the eigenvalue.
Examples & Analogies
Think of it like tuning a musical instrument. When you adjust the tension (the eigenvalue) of a guitar string, it vibrates in a specific way (the eigenvector). By identifying the right tension for the string (what makes it vibrate correctly), you can find the right notes that correspond to that tension, representing how eigenvalues and eigenvectors pair together.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Modal analysis of structures (natural frequencies).
• Stability of equilibrium in mechanical structures.
• Principal stress and strain calculations.
Detailed Explanation
Eigenvalues and eigenvectors play a crucial role in analyzing structures in civil engineering, particularly during modal analysis, where the natural frequencies of structures are determined. Understanding these frequencies helps in predicting how a structure will respond to various forces, ensuring stability and safety. This analysis is essential during the design phase to ensure that buildings can withstand dynamic loads like wind or earthquakes.
Examples & Analogies
Consider a tall building swaying during a heavy storm. By finding the natural frequencies (eigenvalues) and the specific swaying patterns (eigenvectors), engineers can design the structure to minimize the risk of collapse or major damage, similar to how a musical composer would fine-tune an instrument to create harmonious sounds under varying conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: A scalar related to the transformation of a matrix.
-
Eigenvector: A vector that is scaled by a matrix transformation rather than rotated or reflected.
-
Characteristic equation: A formula to find eigenvalues from a matrix.
-
Homogeneous system: A set of linear equations with zero constants.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Given a matrix A and calculated eigenvalue λ, solving (A−λI)v = 0 yields the eigenvector.
-
Example 2: In a truss analysis, eigenvalues derived from stiffness matrices help predict natural frequencies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigen values and vector paths, determine how a matrix casts.
📖 Fascinating Stories
-
In the land of matrices, every vector wanted to explore how they change with different values. They found eigenvalues to guide their paths, scaling but never straying from their direction.
🧠 Other Memory Gems
-
Remember 'E' for Eigen: E = for 'Eigenvalues', V = for 'Vectors'. 'E' helps find 'V'!
🎯 Super Acronyms
MEAS - Matrix Eigenvalues And Solutions, for remembering eigenvalues and their computations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ associated with a linear transformation represented by matrix A, where Av = λv.
-
Term: Eigenvector
Definition:
A non-zero vector v that changes by only a scalar factor when a linear transformation is applied to it.
-
Term: Characteristic equation
Definition:
An equation derived from det(A−λI) = 0 used to find the eigenvalues of a matrix A.
-
Term: Homogeneous system
Definition:
A system of linear equations in which all constant terms are zero.