Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Linear Transformations
Unlock Audio Lesson
Today, we're going to learn about linear transformations. Can anyone tell me what a linear transformation is?
Isn't it some kind of function that changes one vector to another?
Exactly! A linear transformation maps vectors from one vector space to another. What are some properties of these transformations?
It preserves addition and scalar multiplication, right?
Correct! If we have two vectors u and v, and a scalar c, we can say that T(u + v) = T(u) + T(v) and T(cu) = cT(u). Remember this property!
Is there a matrix involved here too?
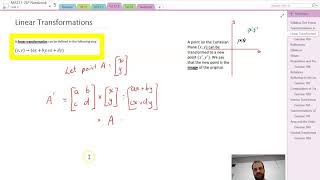
Yes, great question! Every linear transformation can be represented with a matrix. For example, we can express T(x) = Ax, where A is the transformation matrix.
Why is this important, especially in engineering?
In civil engineering, linear transformations help us in analyzing coordinates and understanding how structures behave under different loads. Let's move on to the kernel and range.
Kernel and Range
Unlock Audio Lesson
Can anyone explain what the kernel and range are in the context of linear transformations?
The kernel is where the transformation takes vectors to zero, right?
That's correct! The kernel, or null space, contains all vectors that map to the zero vector under the transformation. And what about the range?
I think it's the set of all possible outputs of the transformation...
Exactly! The range is the image of the transformation. It includes all vectors that can be generated by applying T to any vector in the domain.
How do these concepts link together?
Great question! The Rank-Nullity Theorem shows the relationship between the dimensions of the kernel and the range. It states that the dimension of the kernel plus the dimension of the range equals the dimension of the domain.
Can we remember that with a formula?
Yes, use this: dim(Ker(T)) + dim(Im(T)) = dim(Domain). Understanding this theorem helps to analyze transformations effectively.
Applications in Civil Engineering
Unlock Audio Lesson
Now that we understand the concepts, what are some applications of linear transformations in civil engineering?
Like how we analyze structures?
Exactly! Linear transformations help us convert local coordinates to global ones in a structure. They also aid in stress-strain analysis.
Can you give an example of that?
Sure! When we model the deformation of materials under stress, linear transformations allow us to predict how the material will respond in real-world scenarios.
So, understanding these transformations can lead to safer designs?
Absolutely! That's why linear transformations are crucial in civil engineering. They ensure our structures remain stable and resilient.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the concept of linear transformations, their matrix representations, and the key notions of kernel and range, including the Rank-Nullity Theorem. These concepts are vital for civil engineering applications and understanding the geometric implications of linear mappings.
Detailed
Detailed Summary
Linear transformations are fundamental components of linear algebra that map vectors from one vector space to another while preserving operations of vector addition and scalar multiplication. This section defines a linear transformation mathematically as:
$$T(u+v) = T(u) + T(v)$$
$$T(cu) = cT(u)$$
for vectors u and v, and scalar c. Every linear transformation can be represented by a matrix operation, given by:
$$T(x) = Ax$$
where A is the matrix representation of the transformation and x is the vector being transformed.
Key concepts associated with linear transformations include the kernel (null space), which consists of all vectors that map to the zero vector, and the range (image), which is the collection of all vectors that can be generated by applying the transformation to the vectors in the domain. The Rank-Nullity Theorem connects these concepts by stating:
$$\text{dim(Ker(T))} + \text{dim(Im(T))} = \text{dim(Domain)}$$
This theorem is pivotal in determining the relationships between the dimensions of the kernel and range of a linear transformation.
In civil engineering, linear transformations are applied in coordinate transformations, analysis of deformations, and stress-strain relationships which enhance the understanding of structures under various loads.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Linear Transformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A linear transformation T :V →W between two vector spaces satisfies:
T(u+v)=T(u)+T(v), T(cu)=cT(u)
Detailed Explanation
A linear transformation is a mathematical function that operates between two vector spaces, V and W. It has two main properties that must be satisfied. The first property states that if you take two vectors u and v from vector space V and add them together, the transformation T applied to the sum should equal the transformation applied to each vector individually, meaning T(u + v) = T(u) + T(v). The second property involves scalar multiplication: if you multiply a vector u by a scalar c (a constant number), the transformation T applied to that result should equal the same scalar multiplied by the transformation of the original vector, represented by T(cu) = cT(u). These properties ensure that the transformation preserves the structure and relationships of the original vector spaces.
Examples & Analogies
Think of a linear transformation like a factory that processes raw materials into finished products. The raw materials (vectors from space V) come in various forms, and the factory receives them and uses a consistent set of rules (the transformation) to create finished goods (vectors in space W). Whether you send in one type of raw material on its own or mix two types together, the factory's processes ensure that you always get results that adhere to certain expectations, just like how a linear transformation ensures that properties of addition and scalar multiplication hold.
Matrix Representation of Linear Transformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Every linear transformation can be represented as a matrix acting on a vector:
T(x)=Ax
Detailed Explanation
Every linear transformation can be expressed in terms of matrices, making it easier to work with in applications. Here, T represents the linear transformation, x is a vector in the input space V, and A is a matrix that describes how the transformation is applied to x. The equation T(x) = Ax shows that applying the transformation to the vector x involves multiplying the matrix A by the vector. This matrix representation is powerful, as it allows us to use matrix operations to analyze and compute linear transformations effectively.
Examples & Analogies
Imagine you have a recipe that shows how to transform basic ingredients into a delicious dish. In this analogy, the ingredients represent the input vectors, and the steps in the recipe represent the linear transformation. The matrix A is like the recipe card that captures all the steps in a structured format. When you input your ingredients (the vector x) into the recipe (apply the matrix A), you produce the final dish (the transformed vector T(x)). This structured approach allows cooks (or mathematicians) to reproduce consistent results every time.
Kernel and Range of a Linear Transformation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Kernel (Null Space): Set of all vectors mapped to 0.
• Range (Image): Set of all vectors that are images under T.
Detailed Explanation
In the context of linear transformations, the kernel and range are two important concepts. The kernel (or null space) of a linear transformation refers to the set of all vectors in the domain V that are mapped to the zero vector in the codomain W. In simpler terms, these are the vectors that get 'lost' or transformed into nothing. On the other hand, the range (or image) of a linear transformation is the set of all output vectors in W that are produced by applying the transformation to vectors from V. This means the range gives us the actual vectors that the transformation can produce, showing the effectiveness of the transformation.
Examples & Analogies
Consider a filtering process, like making orange juice. The oranges you put in represent the vectors in your domain, and the juice you get out represents the vectors in your codomain. Some parts of the oranges, like seeds or pulp (the kernel), do not make it through the filter; they are transformed into nothing (the zero vector). The smooth, liquid juice that comes out is the range; it represents all the possible outcomes you can achieve through your filtering process.
Rank-Nullity Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
dim(Ker(T))+dim(Im(T))=dim(Domain)
Detailed Explanation
The rank-nullity theorem is a fundamental theorem in linear algebra that establishes a connection between the kernel, range, and domain of a linear transformation. In this equation, 'dim(Ker(T))' represents the dimension of the kernel (how many vectors are mapped to zero), 'dim(Im(T))' is the dimension of the range (the number of distinct output vectors possible), and 'dim(Domain)' is the dimension of the original space from which the vectors come. The equation shows that the sum of the dimensions of the kernel and the range equals the dimension of the domain, highlighting the balance between what gets lost in transformation and what is produced.
Examples & Analogies
Think of a factory production line where raw materials come in (the domain), and some of those materials are wasted or lost during processing (the kernel), while others turn into finished products (the range). The rank-nullity theorem helps us understand that the total amount of raw materials we start with is equal to the amount that gets lost plus the amount that successfully turns into finished products. This relationship can help managers optimize their processes to minimize waste and maximize output.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Coordinate transformations (local to global system).
• Deformations and stress-strain relationships.
Detailed Explanation
Linear transformations play an essential role in civil engineering applications. One significant use is in coordinate transformations, where engineers must convert coordinates from a localized system (like within a small structure) to a global system (used in larger plans). This is crucial for accurate positioning and alignment when constructing buildings, bridges, or other structures. Another application relates to analyzing how materials deform under stress. Engineers need to understand how forces affect structures, and linear transformations can model stress-strain relationships effectively, ensuring structures maintain integrity.
Examples & Analogies
Imagine a virtual reality system that overlays a designer’s plans onto a real-world site. Just like you might need to transform the coordinates of virtual objects to align them with the real landmarks in a VR environment, civil engineers use linear transformations to accurately position the structures they design. Furthermore, when considering how a bridge bends under load (like cars driving over it), engineers use linear transformations to study stress and strain, ensuring that even under pressure, the bridge will remain safe and functional.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Transformation: A function that maps one vector space to another, preserving addition and scalar multiplication.
-
Kernel: The set of vectors that map to zero, essential in understanding solutions to linear systems.
-
Range: The output set of a linear transformation, indicating what is achievable through the transformation.
-
Rank-Nullity Theorem: A principle that relates the dimensions of the kernel and range of a transformation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Transforming a vector [1, 2] using the matrix A = [[2, 0], [0, 3]] results in a new vector [2, 6].
-
In engineering, converting local coordinates of a structure to global coordinates can involve a linear transformation, helping engineers to analyze loads effectively.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the kernel's space, look for zero's place; dimensions in the range will keep the fitting pace.
📖 Fascinating Stories
-
Imagine a bridge engineer using a transformation to predict how a bridge will sway under pressure. The kernel helps find stabilization pressures while the range predicts movement under stress.
🧠 Other Memory Gems
-
Keep track of "K.R. Dimension" to remember Kernel and Range's dimensional relationship.
🎯 Super Acronyms
Remember 'L.T. K.R.' for Linear Transformation, Kernel, and Range.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Transformation
Definition:
A mapping between vector spaces that preserves vector addition and scalar multiplication.
-
Term: Kernel (Null Space)
Definition:
The set of all vectors that are mapped to the zero vector by a linear transformation.
-
Term: Range (Image)
Definition:
The set of all vectors that can be produced as output by a linear transformation.
-
Term: RankNullity Theorem
Definition:
A theorem that states dim(Ker(T)) + dim(Im(T)) = dim(Domain) for a linear transformation.