Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Water Distribution Network Modeling
Unlock Audio Lesson
Today, we're diving into modeling water distribution networks using linear algebra. Can anyone tell me why modeling is important in civil engineering?
I think it's so we can predict how water will flow and ensure everyone gets water efficiently.
Exactly! We can use systems of linear equations to model the relationships between pipes and nodes in the network. Each node represents a junction, while the pipes connect them.
What do you mean by nodes and pipes in this context?
Great question! Nodes are junction points in the system, while pipes are the connections conveying water. Together, they form a framework that can be analyzed mathematically to optimize water distribution.
So, are these equations similar to the systems we learned about earlier?
Yes! We use a system of equations similar to before, and we can apply methods we have learned, such as matrix solutions, to solve them effectively.
To summarize, understanding our water distribution system through modeling is vital for efficiency and resource management. We’ll explore some specific techniques next.
Solving Systems of Linear Equations
Unlock Audio Lesson
Next, let’s discuss how we can solve the equations we obtain. Have you all heard of the Hardy Cross method?
I don’t think I have; can you explain it?
Sure! The Hardy Cross method is an iterative technique used primarily for flow distribution. It adjusts the flow rates estimated initially until the flow conservation at nodes is achieved. Essentially, we refine our guess until we get accurate results.
So, it’s like refining our initial assumptions through testing?
Exactly! This method continuously improves our flow rates. Remember the acronym FOCUS: 'Flow Conservation Under Systems.' It represents the core purpose of the method.
What about the Newton-Raphson method? How’s that different?
Great question! The Newton-Raphson method is a calculus-based method that handles more complex systems. It considers the derivatives to find better estimates through polynomial equations. Think of it like resolving a riddle step by step.
In summary, both methods help us manage flow effectively in our water distribution networks!
Real-Life Applications
Unlock Audio Lesson
Now that we understand the techniques better, let’s look at some real-life applications. Can someone share how these models might impact our daily lives?
I think ensuring that there's enough water during peak times is crucial!
Precisely! The methods help determine the necessary pipe sizes to accommodate varying demands and prevent shortages. Efficiency and sustainability are paramount.
How do you determine if your model is successful?
Success can be gauged through continuous monitoring and observation. If our predictions match the actual data closely, we know our model is robust. Visualizing data through graphs also helps!
What happens if there are leaks in the system?
That’s an excellent point. The methods can help identify discrepancies in flow rates, which can signify leaks, and aid in repair management.
In conclusion, effectively utilizing models in civil engineering not only promotes efficient water management but also upholds community trust.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The water distribution network case study highlights the application of linear algebra in modeling nodes and pipes through equations, which can be solved using matrix methods like Hardy Cross and Newton-Raphson for effective resource management in civil engineering.
Detailed
Detailed Summary
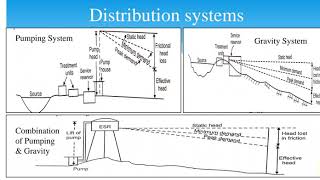
The section on the water distribution network provides a significant example of how linear algebra is utilized in civil engineering to address real-world challenges. In this case, the water distribution network consists of various nodes (representing junctions) and pipes (representing connections) that can be modeled mathematically. Each of these components can lead to a system of linear equations that define how water flows through the network.
The two primary methods discussed for solving these equations include:
- Hardy Cross Method: This iterative method is particularly useful for analyzing the flow distribution in networks. It allows for adjustments to be made to initial flow estimates in such a way that the conservation of flow is maintained at each node.
- Newton-Raphson Method: Though more complex, this technique employs calculus-based iterations to solve nonlinear systems, making it suitable for networks with varying pressures and flow rates.
The effective analysis and management of water distribution systems through these methods underscore the importance of linear algebra in civil engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Modeling of Nodes and Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Nodes and pipes modeled as equations.
Detailed Explanation
In a water distribution network, we represent various points of the system, called nodes (like intersections or taps), and the pipes connecting them. Each node can represent a location where water is either entering, exiting, or being consumed. The flow and pressure at each node can be represented mathematically using equations that model the relationships between flow rates and pressures. A common approach is setting up a system of equations based on the conservation of mass, ensuring that water entering a node equals the water exiting it.
Examples & Analogies
Imagine a road network where cars (water) enter and exit at different intersections (nodes). To understand the traffic flow, we could write equations to track how many cars are entering and leaving each intersection. If one road is blocked, the equations can help us determine how that will affect the flow at surrounding intersections.
Solving Using Matrix Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Solved using matrix methods (e.g., Hardy Cross, Newton-Raphson).
Detailed Explanation
Once the nodes and pipes are modeled into equations, the next step is solving these equations. Matrix methods, such as the Hardy Cross method and Newton-Raphson method, help in finding the flow rates and pressures at each node efficiently. For instance, the Hardy Cross method iteratively balances flows in the network, while Newton-Raphson is a root-finding algorithm that can solve nonlinear equations, providing solutions that converge to the desired flow rates quickly. These methods allow for handling complex systems with multiple variables effectively.
Examples & Analogies
Think of solving these equations like tuning a musical ensemble. Each musician (node) plays a part, but if one is off-key, the others must adjust. The Hardy Cross method is like the conductor guiding the musicians, ensuring everyone stays in harmony using adjustments based on feedback from the audience's (system's) response.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modeling Water Networks: The process of representing water distribution systems mathematically.
-
Flow Distribution: Understanding how water flows through nodes and pipes.
-
Hardy Cross Method: An iterative method refining flow estimates in networks.
-
Newton-Raphson Method: A method for solving nonlinear equations related to network flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modeling a water system with three nodes and two pipes and determining flow rates using the Hardy Cross method.
-
Utilizing the Newton-Raphson method to calculate pressures at nodes in a complex network with changes in elevation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For water flow that must persist, Hardy's method helps us fix the list!
📖 Fascinating Stories
-
Imagine a bustling city with many roads (pipes) where cars (water) must shift and turn at junctions (nodes). Some cars may feel lost; using Hardy's daily inspection helps restore balance.
🧠 Other Memory Gems
-
For flow calculations, think of the acronym 'FLOW': 'Find, Locate, Optimize Water.'
🎯 Super Acronyms
Hardy Cross = HC
- 'Help Conservation'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Nodes
Definition:
Points in a water distribution network representing junctions where the flow can change direction.
-
Term: Pipes
Definition:
Conduits in the system through which water flows, connecting the nodes.
-
Term: Hardy Cross Method
Definition:
An iterative method used for flow distribution analysis in networks.
-
Term: NewtonRaphson Method
Definition:
A calculus-based iterative method for solving nonlinear systems of equations.