Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Matrix Inverses
Unlock Audio Lesson
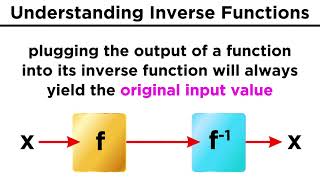
Today, we will explore the concept of the inverse of a matrix. Does anyone know what it means for a matrix to have an inverse?
It means there is another matrix that can 'undo' the effect of the original matrix.
Exactly! If matrix A has an inverse A⁻¹, then multiplying them gives us the identity matrix I. Remember, the identity matrix acts like 1 in multiplication. Can anyone tell me when a matrix is considered non-singular?
A matrix is non-singular if its determinant is not zero.
Great! Since only non-singular matrices have inverses, let's look at methods to find these inverses.
Adjoint Method
Unlock Audio Lesson
First, we have the adjoint method. This involves two steps: finding the determinant and the adjugate of the matrix. Can anyone tell me the formula for the inverse using this method?
It’s A⁻¹ = adj(A) / det(A).
Spot on! Remember that the adjugate involves transposing the cofactor matrix. Let's use this method to find the inverse of a 2x2 matrix as a class exercise.
Could we see how to find the adjugate for the matrix first?
Absolutely, let's calculate the adjugate step by step.
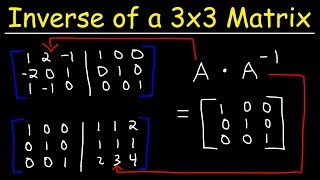
Gauss-Jordan Elimination Method
Unlock Audio Lesson
The second method we'll discuss is the Gauss-Jordan elimination. Can anyone describe how this method works?
It involves transforming the matrix into reduced row-echelon form, right?
Correct! We also attach an identity matrix on the right and perform row operations. If we reach the form where the original matrix turns into the identity, the other side will become the inverse.
Is this method efficient for larger matrices?
Yes, especially when dealing with larger matrices. It provides a systematic approach to finding the inverse. Let’s try an example together.
Applications and Summary
Unlock Audio Lesson
Why do you think it’s important to understand how to find a matrix inverse?
It helps solve systems of linear equations more easily.
And it’s useful in various fields like engineering!
Exactly! Now, to summarize, we can find a matrix's inverse using the adjoint method or the Gauss-Jordan elimination method. Each has its own advantages and use cases.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the significance of matrix inverses in linear algebra and introduces two primary methods for their calculation: the adjoint method and the Gauss-Jordan elimination method. Both methods are critical for solving linear systems and understanding matrix properties.
Detailed
In linear algebra, the concept of the inverse of a matrix is essential for solving systems of equations and understanding matrix relationships. A square matrix A has an inverse denoted as A⁻¹ if it satisfies the equation AA⁻¹ = A⁻¹A = I, where I is the identity matrix. However, an inverse exists only for non-singular matrices, which are matrices with a non-zero determinant. This section details two main methods to find the inverse of a matrix: 1) Adjoint Method, which calculates the inverse using the formula A⁻¹ = (1/det(A)) * adj(A), where adj(A) is the adjugate (or adjoint) of A; and 2) Gauss-Jordan Elimination, which transforms the matrix into reduced row-echelon form to identify the inverse. Mastery of these techniques is crucial for various applications in engineering, especially in solving systems of linear equations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Adjoint Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A−1 = ·adj(A) / det(A)
Detailed Explanation
The Adjoint Method is one way to find the inverse of a matrix A, which is only possible for non-singular matrices (matrices with a non-zero determinant). To find the inverse, you first compute the adjugate (or adjoint) of the matrix, denoted as adj(A). The adjugate matrix is formed by taking the transpose of the cofactor matrix of A. Then, you divide the adjugate by the determinant of A, det(A), which scales the result to get the true inverse. Thus, if det(A) is not zero, you can successfully find the inverse.
Examples & Analogies
Think of the process as making a recipe that requires specific ingredients in a certain ratio. The adjugate is like a concentrated extract of the ingredients, while the determinant is how much of the dish you can prepare. If you can make the recipe (det(A) ≠ 0), you can adjust the concentration of your extract (adj(A)) to get the final dish (the inverse of the matrix) right.
Gauss-Jordan Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Gauss-Jordan Method
Detailed Explanation
The Gauss-Jordan Method is an algorithm used to find the inverse of a matrix through a systematic process of row operations. You begin with the augmented matrix, which is formed by placing the identity matrix of the same size next to matrix A. The goal is to perform elementary row operations (like swapping rows, multiplying a row by a non-zero number, or adding/subtracting rows) to transform the left side (A) into the identity matrix. If you can achieve this, then the right side becomes the inverse of A.
Examples & Analogies
Imagine you are solving a jigsaw puzzle. The pieces of the puzzle represent the elements of the matrix. The objective is to arrange the pieces to form a complete picture (the identity matrix). As you swap pieces and adjust them (applying row operations), you gradually create the image. Once all pieces are in place correctly, the border of the jigsaw puzzle represents the identity, and the internal image represents the inverse of the matrix.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Matrix Inverse: Fundamental for solving linear equations.
-
Non-Singularity: Only non-singular matrices have inverses.
-
Adjoint Method: Uses the adjugate to find the inverse.
-
Gauss-Jordan Method: A systematic approach for matrix inversion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Finding the inverse of a 2x2 matrix using the adjoint method.
-
Using Gauss-Jordan elimination to find the inverse of a 3x3 matrix.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Find the inverse with adjoint, it's quite straightforward, just don't miss the determinant or you'll be cornered!
🎯 Super Acronyms
AGA - Adjoint, Get Det, and Apply the formula.
📖 Fascinating Stories
-
Imagine two best friends, A and its Inverse A⁻¹. They work together, and when they meet, they create the identity I, proving they complete each other.
🧠 Other Memory Gems
-
When calculating inverses, just remember: 'All Good Algebra' – Adjoint first, GCD next!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inverse of a Matrix
Definition:
A matrix A⁻¹ such that AA⁻¹ = A⁻¹A = I, where I is the identity matrix.
-
Term: NonSingular Matrix
Definition:
A matrix with a non-zero determinant, which has an inverse.
-
Term: Adjoint Method
Definition:
A method of finding the inverse of a matrix using its adjugate and determinant.
-
Term: GaussJordan Elimination
Definition:
A method of finding the inverse of a matrix by transforming it into reduced row-echelon form.