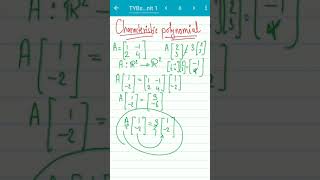
Relation to Characteristic Polynomial
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Minimal Polynomial
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to discuss the minimal polynomial of a matrix. Can anyone tell me what a polynomial is?

Isn't it an expression that includes variables and coefficients?

Correct! Now, the minimal polynomial is a specific kind of polynomial related to matrices. It's defined as the monic polynomial of least degree such that when you substitute your matrix into it, you get the zero matrix, i.e., m(A) = 0.

What do you mean by 'monic'?

Great question! A monic polynomial is one where the leading coefficient is 1. Now, why do you think this is important?

Is it because it simplifies our calculations?

Exactly! A monic polynomial presents a standard format that is easier to work with. Let's remember this concept with the mnemonic 'Minimum Affects Matrix' or MAM!

I'll remember that!

To summarize, the minimal polynomial, which must be monic, gives us essential information about the matrix it represents.
Minimal and Characteristic Polynomial Relationship
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Who can remind me about the characteristic polynomial?

It's the determinant of (A - λI)!

Exactly! Now, a key point is that the minimal polynomial always divides the characteristic polynomial. Can someone explain why this is significant?

It might help in finding eigenvalues, right?

Right again! The roots of the characteristic polynomial give us the eigenvalues of the matrix. Now think about the size of Jordan blocks regarding the minimal polynomial.

Does the degree of the minimal polynomial indicate the size of the largest Jordan block?

Spot on! The degree indeed reflects this. Remember, every degree of the minimal polynomial provides insight into the matrix's structure. Let’s use the acronym JBS (Jordan Block Size) to help remember this.

JBS—a good way to memorize!

In conclusion, understanding the divisibility of the minimal polynomial by the characteristic polynomial is crucial for analyzing the behavior of matrices.
Applications of Minimal Polynomial
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

How do you all think the minimal polynomial can be used in engineering?

Maybe in stability analysis?

Absolutely! The minimal polynomial is valuable in control systems to determine stability.

Can it also be used for structural behavior analysis?

Yes, that’s right! It helps predict how structures respond under various loads. Now, remember the phrase 'Polynomials Build Stability' to recall these applications!

I like that! It helps connect the concept to real-world applications.

To sum up, minimal polynomials have significant applications in both control systems and structural analysis, showing their importance in engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explains the concept of the minimal polynomial relating it to the characteristic polynomial. The minimal polynomial divides the characteristic polynomial, and its degree reflects the size of the largest Jordan block, which is essential for determining diagonalizability in linear algebra and its applications in control systems and structural behavior analysis.
Detailed
Relation to Characteristic Polynomial
The minimal polynomial of a matrix is defined as the monic polynomial of the least degree such that when the matrix is substituted into it, the result is the zero matrix (i.e., \(m(A) = 0\)). Key points include:
- Characteristic Polynomial: The characteristic polynomial \(p(\lambda) = \text{det}(A - \lambda I)\) is significant as it helps find the eigenvalues of a matrix. The roots of this polynomial correspond to eigenvalues.
- Divisibility: The minimal polynomial always divides the characteristic polynomial, providing a relationship between these two polynomials.
- Degree and Jordan Blocks: The degree of the minimal polynomial indicates the size of the largest Jordan block for the corresponding eigenvalue in the Jordan canonical form of the matrix. This is crucial in determining if a matrix can be fully diagonalized.
- Application: The minimal polynomial has vital applications in control systems and structural behavior analysis, impacting stability and system response.
Understanding these concepts allows for deeper insights into the structure and behavior of linear transformations represented by matrices.
Youtube Videos








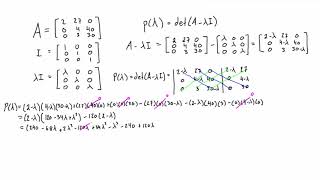
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Minimal Polynomial and Characteristic Polynomial
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Always divides the characteristic polynomial.
Detailed Explanation
The minimal polynomial is a specific polynomial associated with a matrix, and it has the important property of always dividing the characteristic polynomial. This means that any root (eigenvalue) of the minimal polynomial is also a root of the characteristic polynomial, but the minimal polynomial is the simplest (of the lowest degree) polynomial that satisfies m(A) = 0 for a given matrix A.
Examples & Analogies
Think of the minimal polynomial like the simplest recipe you can use to make a specific dish. The characteristic polynomial is like a more complex version of that recipe that includes all the ingredients, while the minimal polynomial is a simpler version that still gets the job done.
Degree of Minimal Polynomial
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Degree of minimal polynomial gives the size of the largest Jordan block.
Detailed Explanation
The degree of the minimal polynomial provides critical information about the structure of the matrix concerning its Jordan form. Specifically, it indicates the size of the largest Jordan block associated with the eigenvalue of the matrix. A Jordan block corresponds to a group of eigenvectors that share a common eigenvalue, and this degree tells us how these eigenvectors are organized.
Examples & Analogies
Imagine building a tower from blocks. The bigger the block you start with (analogous to the degree of the minimal polynomial), the larger the section of the tower you can build without needing additional support from smaller blocks. Similarly, in matrices, a higher degree minimal polynomial means a more complex interrelationship among eigenvectors.
Applications of Minimal Polynomial
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Helps in determining diagonalizability.
• Essential in control systems and structural behavior analysis.
Detailed Explanation
The minimal polynomial is crucial in various applications, particularly in determining whether a matrix can be diagonalized. A matrix is diagonalizable if it has a minimal polynomial whose roots (eigenvalues) are distinct. Additionally, in control systems and structural analysis, the minimal polynomial helps us understand system behavior and stability.
Examples & Analogies
Think of diagonalizability as organizing your books on a shelf in an easy-to-reach manner versus a disorganized pile. Diagonalizable matrices allow for simpler calculations, just like having books arranged by genre makes finding the right one faster. In engineering, this translates to efficiently analyzing dynamic systems, such as how a bridge reacts under load.
Key Concepts
-
Minimal Polynomial: The polynomial that indicates the matrix's eigenvalues' structure and directly relates to the characteristic polynomial.
-
Characteristic Polynomial: A polynomial that is fundamental in finding the eigenvalues of the matrix.
-
Divisibility: The minimal polynomial always divides the characteristic polynomial, impacting the matrix structure.
-
Jordan Block Size: The degree of the minimal polynomial represents the largest Jordan block for corresponding eigenvalues.
Examples & Applications
Finding the minimal polynomial for a given 2x2 matrix and observing how it divides the characteristic polynomial.
Evaluating a characteristic polynomial and determining eigenvalues, then using the minimal polynomial to verify stability conditions in control systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the roots, we need the square, The minimal polynomial shows we care!
Stories
Once a matrix ventured alone, seeking its roots. It found its minimal polynomial, the guide that knew the way, leading it back home to stability.
Memory Tools
MAM - Minimum Affects Matrix: Helped remember 'Minimal polynomial = Monic, Affects structure'.
Acronyms
JBS - Jordan Block Size
Helps recall that the degree tells us the largest block size!
Flash Cards
Glossary
- Minimal Polynomial
The monic polynomial of least degree such that m(A) = 0 when substituting matrix A into it.
- Characteristic Polynomial
A polynomial defined as det(A - λI), used to find the eigenvalues of matrix A.
- Jordan Block
A square matrix representing an eigenvalue in tree-like structure formation, significant in the Jordan canonical form.
Reference links
Supplementary resources to enhance your learning experience.
