Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Iterative Methods
Unlock Audio Lesson
Today, we will explore iterative methods, starting with why they are important. Can anyone tell me why direct methods may not always be the best option?
They take too long for large systems, right?
Exactly! When we have large systems, like those in civil engineering projects, direct methods become impractical. What do you think are some common iterative methods?
I think Gauss-Seidel is one of them.
Correct! Gauss-Seidel is a popular choice. Let's remember it with the acronym **G**ood **S**olutions **M**ethod. Any other methods you recall?
What about the Jacobi method?
Exactly! The Jacobi method is another iterative method. It calculates using the previous iteration values. Let's summarize: Gauss-Seidel and Jacobi are common iterative methods to handle large systems efficiently.
Sparse Matrices and their Importance
Unlock Audio Lesson
Now that we've understood some methods, let's discuss sparse matrices. Who can define what a sparse matrix is?
Isn't it a matrix with a lot of zeros?
Exactly! Sparse matrices contain many zero elements, which is common in finite element models. Why do you think understanding sparse matrices is crucial?
Because it helps in saving memory and computational costs?
Right! We need to maximize efficiency in handling these matrices while implementing iterative methods. This leads us to think about how to store and process large systems.
Would that also relate to how computers optimize calculations?
Absolutely! Efficient algorithms and storage strategies come into play. Remember: efficiency is key when dealing with sparse matrices!
Applications of Iterative Methods in Engineering
Unlock Audio Lesson
Let’s dive into the applications of iterative methods in civil engineering. Why do you think these methods matter in our field?
Because we deal with big systems like bridges or buildings?
Precisely! Issues like structural analysis often involve massive equations where iterative methods become indispensable. Can anyone think of some scenarios where we might use these methods?
Maybe during the analysis of stress and strain in structures?
Great example! Stress analysis is one practical application. Also, fluid dynamics in large systems can employ iterative methods effectively, representing a vast importance in structural design and stability.
So, it’s about efficiency in solving real-world problems?
Exactly! Efficiency and accuracy are enhanced through the use of iterative methods in engineering challenges.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces iterative methods such as Gauss-Seidel, Jacobi, and Successive Over-Relaxation (SOR) as effective solutions for large systems where direct methods may be impractical. The discussion includes the significance of sparse matrices commonly encountered in finite element models and highlights the need for specific solution strategies.
Detailed
Iterative Methods in Linear Algebra
In the realm of Linear Algebra, direct algebraic solutions for systems with a significant number of equations can be impractical; hence, iterative methods provide a viable alternative. This section primarily focuses on these methods, which are critical for civil engineering applications, especially when dealing with large-scale problems such as structural analysis or fluid dynamics.
Key Types of Iterative Methods
- Gauss-Seidel Method: This method updates the solution iteratively, using the newest values as soon as they are available, thereby potentially accelerating convergence.
- Jacobi Method: Unlike Gauss-Seidel, this method computes the next iteration using values from the previous iteration, which can be more suitable when parallel processing is required.
- Successive Over-Relaxation (SOR): This technique is an enhancement of the Gauss-Seidel method and includes a relaxation factor to expedite convergence further.
Importance of Sparse Matrices
The discussion also emphasizes sparse matrices, which contain a significant number of zero elements and are prevalent in finite element analysis. Efficient handling of sparse matrices is essential to minimize storage and computational costs, making iterative methods even more relevant in engineering applications. These methods must be optimized for effective memory usage, which is crucial for large-scale problems, underscoring the intersection of linear algebra and computational engineering.
Youtube Videos
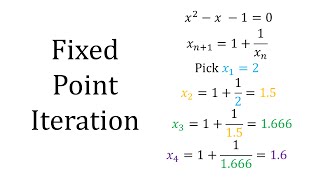
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Iterative Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Iterative Methods
• Gauss-Seidel Method
• Jacobi Method
• Successive Over Relaxation (SOR)
Detailed Explanation
Iterative methods are techniques used to find approximate solutions to mathematical problems, particularly useful for very large systems of equations. They work by starting with an initial guess and then refining that guess repeatedly until the solution converges to an acceptable level of accuracy.
There are various types of iterative methods, including the Gauss-Seidel method, Jacobi method, and Successive Over Relaxation (SOR). Each method has its own way of updating the solution based on previous guesses, aiming to reach stability and convergence.
Examples & Analogies
Imagine trying to adjust the temperature of your home. You start with a guess (say, setting the thermostat to 70°F), but you quickly realize it's too hot. So, you adjust it down to 68°F and wait for a bit. After some time, if it's still too hot, you adjust again to 67°F. Each adjustment is based on your previous guess, much like how iterative methods refine their solutions until you reach the desired comfort level.
The Gauss-Seidel Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Gauss-Seidel Method
Detailed Explanation
The Gauss-Seidel method is an iterative technique used specifically for solving systems of linear equations. It operates by taking one equation at a time and using the most recent values of variables. When solving for a particular variable, it substitutes in already updated values for the other variables, allowing for faster convergence. This method is particularly effective when the matrix of coefficients is diagonally dominant.
Examples & Analogies
Think of the Gauss-Seidel method like making adjustments to a recipe. If you're baking a cake and you taste the batter, you notice it is too sweet. Instead of waiting to finish all mixing before adjusting, you immediately add some lemon juice to balance the flavor. Each tasting and adjustment reflects your latest refined judgment, similar to how Gauss-Seidel uses the latest variable values to update its solution.
The Jacobi Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Jacobi Method
Detailed Explanation
The Jacobi method is another iterative method that updates all variable values simultaneously, using the values from the previous iteration. It does not rely on the most recent updates, which can lead to slower convergence compared to the Gauss-Seidel method, especially for non-diagonally dominant matrices. However, it is fully parallelizable, which allows multiple computations to be performed at the same time, making it suitable for use in modern computing environments.
Examples & Analogies
Imagine a group of friends trying to solve a puzzle together. Each friend works on their own piece of the puzzle simultaneously, communicating only at the end to check how well their individual pieces fit. They are all taking their previous knowledge into account but aren’t updating their placements based on each other's work during their individual attempts. This is how the Jacobi method functions—updating all values independently rather than relying on the latest information.
Successive Over Relaxation (SOR)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Successive Over Relaxation (SOR)
Detailed Explanation
Successive Over Relaxation (SOR) is a modified version of the Gauss-Seidel method designed to speed up convergence. It introduces a relaxation factor, which effectively controls the amount by which the new solution should be adjusted towards the computed values. The idea is to overshoot a little to reach the solution faster. By selecting an optimal relaxation factor, SOR can significantly reduce the number of iterations needed to reach a given accuracy.
Examples & Analogies
Think of SOR like adjusting your aim while shooting basketball. Instead of just trying to hit the target with perfect precision, you decide to take a small calculated risk and aim a little higher or lower based on your previous shots to determine how you can improve your accuracy, gradually honing in on the basket faster than if you were just adjusting based on your last attempt.
Sparse Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Sparse Matrices
• Matrices with a large number of zero elements.
• Common in Finite Element Models (FEM).
• Require special storage and solution strategies to save memory and computational cost.
Detailed Explanation
Sparse matrices are matrices that contain a significant number of zero entries. In large-scale engineering problems and particularly in computational applications like Finite Element Models (FEM), sparse matrices arise due to their structure. Because storing all elements of a large matrix can consume significant memory, efficient algorithms and storage methods are often developed to handle only the non-zero elements, reducing both memory usage and computational demand.
Examples & Analogies
Imagine managing a warehouse filled with boxes. If most of the boxes are empty (zero items), it would be inefficient to label every box. Instead, you only label the boxes that contain items, which saves space and makes it easier to locate what you need. This is akin to how sparse matrices operate—they focus on just the essential non-empty elements to simplify storage and processing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Iterative Methods: Techniques to find solutions through repeated approximations.
-
Gauss-Seidel Method: Updates solutions using the latest values for faster convergence.
-
Jacobi Method: Calculates with older values, making it suitable for parallel processes.
-
Successive Over-Relaxation: Improves convergence speed of Gauss-Seidel.
-
Sparse Matrices: Large matrices with many zero elements that require special handling.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A civil engineer uses the Gauss-Seidel method to analyze load distribution in a bridge's support structure, simplifying complex equations into manageable iterative solutions.
-
In fluid dynamics modeling, the Jacobi method is utilized to simulate water flow in a large network of conduits, where iterative calculations improve efficiency and reduce computation time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To solve large sums with ease, Gauss-Seidel makes it a breeze; while Jacobi takes it slow, still gets results in a steady flow.
📖 Fascinating Stories
-
Imagine a busy construction site where engineers solve load distributions like puzzles, using the Gauss-Seidel method to piece the right values together quickly, while Jacobi lets them take their time, ensuring accuracy through careful iteration.
🧠 Other Memory Gems
-
Remember Good Solutions in Methods (Gauss-Seidel, SOR, etc.) for thinking about iterative solutions.
🎯 Super Acronyms
Use **J**ust **S**olve **O**ne (Jacobi, SOR) to remember types of iterative methods that focus on solving equations iteratively.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Iterative Methods
Definition:
Procedures that repeatedly refine estimates to find solutions to equations, particularly in large systems.
-
Term: GaussSeidel Method
Definition:
An iterative method that updates the solution vector by using newly computed values immediately.
-
Term: Jacobi Method
Definition:
An iterative method where the next iteration uses the previous iteration’s values for all variables.
-
Term: Successive OverRelaxation (SOR)
Definition:
An enhanced version of the Gauss-Seidel method that accelerates convergence using a relaxation factor.
-
Term: Sparse Matrix
Definition:
A matrix in which the majority of its elements are zero, requiring specialized storage and calculation techniques.