Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Eigenvalues and Eigenvectors
Unlock Audio Lesson
Today, we’re exploring definitions. For a square matrix A, an eigenvalue λ and eigenvector v satisfy the equation Av = λv. Can anyone tell me what the significance of this definition is?
Does it mean that the transformation defined by A stretches or compresses the vector v without changing its direction?
Exactly! We can think of eigenvalues as factors indicating how much the associated eigenvector is stretched or shrunk. This leads us to the practical utilities of these concepts in engineering.
So, every transformation can have multiple eigenvalues and corresponding eigenvectors?
That’s right, Student_2! The number of unique eigenvalues corresponds to different stretching effects on vectors in the space defined by the matrix.
Finding Eigenvalues
Unlock Audio Lesson
To find eigenvalues, we use the characteristic equation, which is found by calculating the determinant of A - λI. Can anyone remind me what I stands for?
I is the identity matrix, right?
Correct! Now, solving this determinant equation, det(A - λI) = 0, gives us the eigenvalues. Who can share why this is quadratic in nature for a 2x2 matrix?
I think it’s because the determinant of a 2x2 matrix involves the product and subtraction of terms?
Exactly! By setting the determinant to zero, we can uncover the eigenvalues that tell us about the behaviors of the transformation. Let’s apply this in some problems!
Finding Eigenvectors
Unlock Audio Lesson
Now, after we have eigenvalues, how do we find the corresponding eigenvectors?
By plugging the eigenvalue λ back into the equation (A - λI)v = 0, right?
Spot on, Student_1! This equation must satisfy any non-zero vector v that is stretched by the transformation. Why do we want v to be non-zero?
Because we need meaningful vectors that represent directions in the space!
Exactly! And understanding these vectors is crucial for applications like stability analysis in civil engineering. Let’s go through a practice problem together.
Applications in Civil Engineering
Unlock Audio Lesson
So, why are eigenvalues and eigenvectors important in civil engineering?
I guess they can help analyze the natural frequencies of structures!
Correct! This analysis is crucial for ensuring stability. For example, understanding how structures respond to vibrations can prevent failures during earthquakes.
And they can be used to compute principal stresses in materials, right?
Absolutely! These practical applications emphasize why we must master these concepts. Does anyone see how this knowledge might apply to real-world projects?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvalues and eigenvectors are critical concepts in linear algebra, defined in relation to a square matrix. The section outlines how to find eigenvalues through the characteristic equation and eigenvectors via a linear transformation. Applications in civil engineering are discussed, underscoring their importance in structural analysis and stability assessments.
Detailed
Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are fundamental concepts in linear algebra, especially when dealing with square matrices. An eigenvalue, denoted as λ, is a scalar associated with a square matrix A, which transforms a corresponding non-zero vector v into a scalar multiple of itself according to the equation:
$$ Av = λv $$
Here, v is termed as the eigenvector of A linked to the eigenvalue λ. To find eigenvalues, one must solve the characteristic equation:
$$ det(A - λI) = 0 $$
where I is the identity matrix. Once eigenvalues are determined, eigenvectors can be computed by solving:
$$ (A - λI)v = 0 $$
These concepts are not merely abstract; they hold significant applications in civil engineering, particularly in modal analysis for determining natural frequencies of structures, analyzing stability, and calculating principal stresses and strains. Thus, understanding eigenvalues and eigenvectors equips civil engineers with essential tools for assessing and ensuring structural integrity.
Youtube Videos
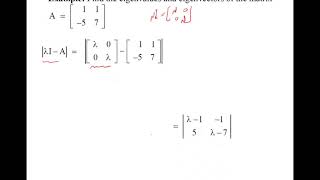
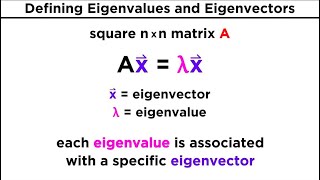
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a square matrix A, a non-zero vector v and scalar λ such that:
$$Av = λv$$
Here, λ is called the eigenvalue and v is the eigenvector.
Detailed Explanation
In linear algebra, an eigenvalue relates to a special type of linear transformation. When we apply the matrix A to an eigenvector v, the result is simply the eigenvector scaled by a factor λ, known as the eigenvalue. This means that the direction of v doesn't change; it is only stretched or shrunk. Understanding this relationship helps in various applications, such as stability analysis and modal analysis.
Examples & Analogies
Imagine a rubber band (the eigenvector) that you can stretch. When you pull it (applying the matrix), it gets longer or shorter but keeps pointing in the same direction. The amount you stretch it by is like the eigenvalue.
Finding Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solve the characteristic equation:
$$det(A−λI)=0$$
Detailed Explanation
To find the eigenvalues, we need to set up and solve the characteristic equation. This equation is derived from the determinant of (A - λI) being zero. Here, I is the identity matrix, and the determinant represents a scaling factor of the transformation. Solving this equation gives us the possible eigenvalues for the matrix A.
Examples & Analogies
Think of the determinant as the volume of a shape. When we say the volume is zero, it means the shape collapses into a flat pancake. This 'collapse' condition gives us the eigenvalues, representing points where the transformation changes significantly.
Finding Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solve:
$$(A−λI)v =0$$
Detailed Explanation
Once we have the eigenvalues, we can find the corresponding eigenvectors by plugging these values back into the equation (A - λI)v = 0. This task involves solving a homogeneous system of linear equations, which yields the vectors that satisfy the relationship defined by the eigenvalue.
Examples & Analogies
Using our example from earlier, if you know how much to stretch the rubber band (the eigenvalue), you can determine all the positions of the rubber band (the eigenvectors) at which it maintains the same direction under that stretch.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Modal analysis of structures (natural frequencies).
- Stability of equilibrium in mechanical structures.
- Principal stress and strain calculations.
Detailed Explanation
Eigenvalues and eigenvectors play crucial roles in civil engineering, particularly in analyzing structures and mechanical systems. For example, during modal analysis, engineers use eigenvalues to determine the natural frequencies at which a structure will resonate. This information is critical for ensuring that structures can withstand vibrations from external forces, such as wind or earthquakes.
Examples & Analogies
Consider a swing. If you push it at its natural frequency, it goes higher and higher—this is similar to how structures can amplify vibrations at certain frequencies (eigenvalues), potentially leading to failure if not accounted for in design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: A scalar indicating how much an eigenvector is transformed.
-
Eigenvector: A vector that remains in its span under a linear transformation.
-
Characteristic equation: An equation used to find eigenvalues.
-
Non-zero vector: Requires eigenvectors to have meaning in the context of transformations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
To find the eigenvalues of a matrix, say A = [[2, 1], [1, 2]], we solve the equation det(A - λI) = 0.
-
In engineering applications, eigenvalues can indicate natural frequencies of a structural system.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues are bold and grand, stretch a vector, lend a hand.
📖 Fascinating Stories
-
Imagine a building shaking during an earthquake, the eigenvalues predict how it will sway based on its design. Each eigenvector shows a unique sway pattern.
🧠 Other Memory Gems
-
L.E.A.N. - Linear equations reveal eigenvalue attributes, Definitions, Applications, Numbers.
🎯 Super Acronyms
EVE - Eigenvalues stretch Vectors Ever so lightly.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ associated with a square matrix A indicating how an eigenvector is stretched or compressed by the transformation.
-
Term: Eigenvector
Definition:
A non-zero vector v that, when transformed by a matrix A, results in a scalar multiple of itself.
-
Term: Characteristic equation
Definition:
An equation derived from the determinant of A - λI, used to find eigenvalues.
-
Term: Identity matrix
Definition:
A square matrix with ones on the diagonal and zeros elsewhere, denoted as I.