Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvalues
Unlock Audio Lesson
Today, we will learn about eigenvalues. So, can anyone tell me what an eigenvalue is?
Is it a special kind of number related to a matrix?
That's right! An eigenvalue is a scalar that describes how a linear transformation affects vectors. We use it specifically in the equation Av = λv, where v is the eigenvector.
So, is it true that eigenvectors are scaled by eigenvalues?
Exactly! The matrix A scales eigenvectors by the corresponding eigenvalue without changing their direction.
How do we actually find these eigenvalues from a matrix?
Great question! To find eigenvalues, we solve the characteristic equation: det(A - λI) = 0. This will give us a polynomial equation.
I see! So the solutions to that equation are the eigenvalues?
Correct! Let’s summarize: eigenvalues are scalars that tell us how matrices transform certain vectors, and we find them using the determinant.
Applications of Eigenvalues
Unlock Audio Lesson
Now that we know how to find eigenvalues, can anyone think of where they might be used in civil engineering?
In analyzing structures, right? For example, determining how they respond to vibrations?
Absolutely! The eigenvalues can help determine natural frequencies in structural analysis.
And what about stability? Do eigenvalues play a role there too?
Yes, they do! Eigenvalues indicate stability conditions of a system. If an eigenvalue has a positive real part, the system may be unstable.
That sounds really important for ensuring safety in engineering projects.
Indeed! Understanding and correctly calculating eigenvalues can significantly affect decisions in design and safety.
So, they can also help in stress calculations?
Exactly! Eigenvalues help determine principal stresses, which are crucial for ensuring structural integrity.
Finding Eigenvalues Step-by-Step
Unlock Audio Lesson
"Let's work through a practical example of finding eigenvalues. Consider the matrix A:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the definitions and the fundamental technique for finding eigenvalues of a square matrix through the characteristic equation. The significance of eigenvalues in various applications, particularly in civil engineering, is also highlighted.
Detailed
Finding Eigenvalues
Eigenvalues are a key concept in linear algebra, particularly important for understanding the behavior of linear transformations. For a given square matrix A, an eigenvector v is a non-zero vector such that when A acts on v, it scales the vector without changing its direction, defined by the equation:
$$Av = λv$$
Here, λ is the eigenvalue corresponding to the eigenvector v. To find the eigenvalues of a matrix, we solve the characteristic equation, which is given by:
$$ ext{det}(A - λI) = 0$$
Where I is the identity matrix of the same dimension as A. The roots of this polynomial will yield the eigenvalues. Eigenvalues play a critical role in various applications such as stability analysis, vibrations in structures, and stress calculations in engineering. This section provides the foundational understanding necessary for applying these concepts effectively.
Youtube Videos
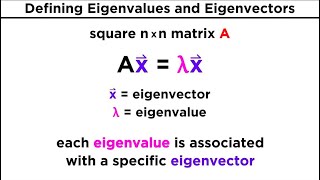
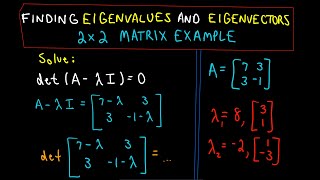
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a square matrix A, a non-zero vector v and scalar λ such that:
Av = λv
Here, λ is called the eigenvalue and v is the eigenvector.
Detailed Explanation
In linear algebra, eigenvalues and eigenvectors are fundamental concepts associated with linear transformations. The equation 'Av = λv' describes how a square matrix 'A' transforms a vector 'v'. If 'v' is an eigenvector, then instead of being transformed to a completely different direction, it is only scaled by a factor of 'λ' (the eigenvalue). This means the direction of 'v' remains unchanged while its length may change based on 'λ'. Understanding this relationship is crucial for simplifying complex linear transformations.
Examples & Analogies
Think of an eigenvector as a compass needle pointing in a specific direction. When you apply a transformation (like rotating or stretching), if the needle is an eigenvector, it will still point in the same direction, but it might get longer or shorter depending on the eigenvalue. Thus, eigenvectors give us directions in which transformations act like simple scaling.
Finding Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solve the characteristic equation:
det(A − λI) = 0
Detailed Explanation
To find the eigenvalues of a matrix 'A', we first need to compute the characteristic equation, which is obtained from the determinant of 'A - λI'. Here, 'I' is the identity matrix of the same size as 'A', and 'λ' is a scalar (the eigenvalue we're trying to find). The determinant, when set to zero, provides a polynomial equation in terms of λ. The solutions to this polynomial provide us with the eigenvalues of the matrix. This process is essential as it allows us to identify the special scalars at which the linear transformation behaves in a uniquely simplified manner.
Examples & Analogies
Imagine you are trying to find the roots of a function, similar to finding where a line crosses the x-axis. In the context of the characteristic equation, we want to see at which points (values of λ) does the multiplication of the transformed vector 'A - λI' yield zero, indicating a special transformation behavior.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Modal analysis of structures (natural frequencies).
• Stability of equilibrium in mechanical structures.
• Principal stress and strain calculations.
Detailed Explanation
The eigenvalues have significant applications in civil engineering, especially when analyzing structures. Specifically, eigenvalues help determine the natural frequencies of a structure (modal analysis), which is critical for ensuring that buildings can withstand vibrations from environmental forces, such as earthquakes. Additionally, knowing the eigenvalues aids in assessing the stability of structures and calculating principal stresses and strains, thus ensuring safety and efficiency in design.
Examples & Analogies
Consider a swing in a playground. When you push it, it has a specific frequency at which it naturally swings back and forth (the natural frequency). If a gust of wind hits it at that frequency, it will swing higher – this is akin to how structures can resonate at certain frequencies identified by their eigenvalues. Understanding these frequencies ensures engineers can design structures that don’t fail during such occurrences.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues: Scalars indicating the factor by which eigenvectors are stretched or compressed during transformations.
-
Eigenvectors: Vectors that maintain their direction despite transformations, related to the scaling factor of eigenvalues.
-
Characteristic Equation: The equation derived from det(A - λI) = 0 to find eigenvalues.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A = [[4,1],[2,3]], the characteristic equation becomes λ^2 - 7λ + 10 = 0, with eigenvalues λ=5 and λ=2.
-
In structural analysis, an eigenvalue may represent the natural frequency of a building, indicating its vibrational response.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalue, eigenvector, in transformation they connect; the matrix gives the power, but eigenvalues protect.
📖 Fascinating Stories
-
Once in the land of matrices, there were heroes known as eigenvectors. The wise wizard, Eigenvalue, would scale them, ensuring they kept their direction as they wandered through transformations.
🧠 Other Memory Gems
-
Remember: 'E' for eigenvalue, 'E' for effect. They scale but do not bend, with every vector they connect.
🎯 Super Acronyms
E = Eigenvalue, V = Vector; Always scale, never defect.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar that indicates how much an eigenvector is stretched or compressed during a linear transformation.
-
Term: Eigenvector
Definition:
A non-zero vector whose direction remains unchanged when a linear transformation is applied.
-
Term: Characteristic Equation
Definition:
An equation formed from the determinant of a matrix subtracted by λ times the identity matrix, used to find eigenvalues.
-
Term: Determinant
Definition:
A scalar value that can be computed from the elements of a square matrix, providing important properties about the matrix.