Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Diagonalizability
Unlock Audio Lesson
Today, we’ll learn about diagonalizability. A matrix is diagonalizable if it can be expressed in a specific form involving its eigenvalues and eigenvectors. Can anyone tell me what it means for a matrix to be diagonalizable?
I think it means the matrix can be simplified into a diagonal form.
Exactly right! This simplification makes computations easier. Does anyone know how we can determine if a matrix is diagonalizable?
We need to check if it has linearly independent eigenvectors.
Very good! If a matrix has n linearly independent eigenvectors, it is diagonalizable.
What if it doesn’t have enough independent eigenvectors?
If it doesn't, then it cannot be diagonalized easily, which can complicate our computations.
So, all distinct eigenvalues can guarantee diagonalizability?
Yes, that’s correct! Distinct eigenvalues inherently lead to a full set of linearly independent eigenvectors.
Let’s summarize: A matrix is diagonalizable if it has n linearly independent eigenvectors, or if all its eigenvalues are distinct. This is essential for simplifying processes, especially in engineering applications. Next, we’ll explore how these concepts can apply to engineering problems.
Applications of Diagonalization
Unlock Audio Lesson
Now that we understand the conditions for diagonalizability, let’s look at how this knowledge applies in civil engineering?
How does it help with solving systems of differential equations?
Great question! Diagonalization allows us to solve linear differential equations more easily by transforming the system into a diagonal form, simplifying the problem dramatically. Can anyone think of a specific application?
Modal analysis of structures, like finding the natural frequencies!
Exactly! Diagonalization is pivotal in modal analysis for assessing the vibration characteristics of structures. This understanding helps engineers design safer structures.
Why is it important to raise matrices to powers?
Raising a matrix to a power is crucial in various simulations and models, including structural and dynamic systems. If we have **A = PDP^{-1}**, then finding **A^k = PD^k P^{-1}** is straightforward.
Let’s recall: Diagonalization not only simplifies computations but is also vital for structural and engineering applications, ensuring that we can efficiently analyze stability and dynamic behaviors.
Recap and Understanding
Unlock Audio Lesson
Before we finish, let’s recap the key points. What are the main conditions for a matrix to be diagonalizable?
It must have n linearly independent eigenvectors!
And if it has distinct eigenvalues!
Correct! How does knowing if a matrix is diagonalizable help in engineering tasks?
It helps simplify computations like solving differential equations!
And applying it to modal analysis!
Exactly! This understanding is fundamental in many engineering challenges. Ensuring we know when and how to apply diagonalization allows us to be more effective in our problem-solving. Let’s wrap up by discussing any questions you might have on today’s topic.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
A matrix is diagonalizable if it has n linearly independent eigenvectors or all its eigenvalues are distinct. This condition simplifies computations, such as raising matrices to powers and solving differential equations.
Detailed
Conditions for Diagonalizability
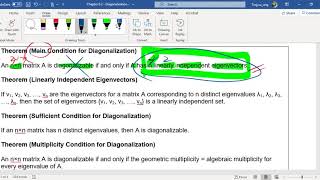
A square matrix A is diagonalizable if it can be expressed in the form A = PDP^{-1}, where D is a diagonal matrix and P is a matrix that contains the eigenvectors of A. For an n x n matrix to be diagonalizable, it must satisfy specific conditions:
- Existence of Linearly Independent Eigenvectors: The matrix must have n linearly independent eigenvectors. This means if you solve for the eigenvalues and eigenvectors, you should be able to form n vectors that are not linear combinations of each other.
- Distinct Eigenvalues: If all eigenvalues of the matrix are distinct, this inherently guarantees diagonalizability since it ensures that you can find a unique eigenvector corresponding to each eigenvalue, leading to a full set of linearly independent eigenvectors.
Importance
Understanding these conditions is crucial for simplifying matrix computations, such as raising a matrix to an integer power (e.g., A^k = PD^kP^{-1}) and solving linear differential equations effectively. In civil engineering and structural analysis, diagonalization facilitates the modal analysis of structures by helping identify vibration modes and stability characteristics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Linear Independence of Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Matrix must have n linearly independent eigenvectors (for an n×n matrix).
Detailed Explanation
A matrix can only be diagonalized if it has 'n' linearly independent eigenvectors. This means that for an n×n matrix, we need n unique eigenvectors that cannot be expressed as a linear combination of each other. If the eigenvectors are independent, they form a 'basis' for the space, allowing us to represent every vector in that space as a combination of the eigenvectors.
Examples & Analogies
Imagine you have a set of tools, like a screwdriver, a wrench, and a hammer. If you want to build something complex, using these independent tools is essential because each serves a different purpose. If one tool could perform the function of another, it wouldn't be as useful. Similarly, we need different, independent eigenvectors to span the entire space.
Distinct Eigenvalues and Diagonalizability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• All distinct eigenvalues imply diagonalizability.
Detailed Explanation
When a matrix has all distinct eigenvalues, it means that each eigenvalue corresponds to a unique eigenvector. This uniqueness ensures that these vectors can be used for diagonalization. Essentially, if we have a matrix with n distinct eigenvalues, we can confidently say that it is diagonalizable because we can extract n linearly independent eigenvectors from it.
Examples & Analogies
Think of a classroom filled with students. If every student (eigenvalue) has a unique hobby (eigenvector), it’s easy to organize them into groups based on their activities. However, if several students have the same hobby, it becomes tricky to group them independently since their hobbies overlap. In this scenario, unique hobbies correspond to unique eigenvalues that allow for clear grouping.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Diagonalizability: A matrix being expressible in the form A = PDP^{-1}.
-
Eigenvectors: Vectors that retain their direction under transformation.
-
Eigenvalues: Scalars indicating how eigenvectors are scaled.
-
Linearly Independent: Vectors not expressible by a combination of others.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a matrix has eigenvalues 2, 3, and 4, then if these are distinct, it will likely be diagonalizable.
-
A matrix with repeated eigenvalues but fewer than n linearly independent eigenvectors is not diagonalizable.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To diagonalize, keep eigenvectors unique, combine them nice, and that's the technique!
📖 Fascinating Stories
-
Imagine a city represented by roads and buildings; if every pathway (eigenvector) is unique, you can easily see the layout (diagonal form).
🧠 Other Memory Gems
-
D.i.a.g.o.n.a.l: Distinct eigenvalues guarantee all necessary eigenvectors.
🎯 Super Acronyms
L.E.A.D
- Linearly Independent Eigenvectors Are Diagonalizable.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonalizable Matrix
Definition:
A matrix that can be expressed in the form A = PDP^{-1}, where D is a diagonal matrix.
-
Term: Eigenvector
Definition:
A non-zero vector that changes at most by a scalar factor when a linear transformation is applied.
-
Term: Eigenvalue
Definition:
A scalar that indicates how much an eigenvector is scaled during the transformation.
-
Term: Linearly Independent
Definition:
A set of vectors is linearly independent if no vector in the set can be expressed as a linear combination of the others.
-
Term: Matrix Powers
Definition:
The product of a matrix multiplied by itself a certain number of times.