Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vector Spaces
Unlock Audio Lesson
Today, let's dive into vector spaces. A vector space is a set of vectors along with two operations: vector addition and scalar multiplication. Can anyone tell me what properties these operations must satisfy?
Does it have to be closed under addition and scalar multiplication?
Exactly! Closure is fundamental. We also have properties like associativity, the existence of an additive identity, and inverses. These properties ensure the structure we need. Can anyone give me an example of a vector space?
The set of all 2D vectors seems like a good example!
Great example! It consists of all vectors of the form (x, y). Any questions on vector spaces so far?
Defining Subspaces
Unlock Audio Lesson
Now, let's discuss subspaces. What do you think a subspace is?
Is it like a smaller vector space within a larger one that follows the same rules?
Exactly! A subspace must itself be a vector space under the same operations. What conditions do you think a subset must meet to be a subspace?
It should be closed under addition and scalar multiplication, and contain the zero vector.
Correct! Remember the zero vector is key. For example, consider all vectors that lie on a line through the origin; that is a subspace. Any other thoughts?
Basis and Dimension
Unlock Audio Lesson
Let's explore basis and dimension. What is a basis?
A basis is a set of linearly independent vectors that span the space.
Right! And the dimension is the number of vectors in that set. Can someone explain why this is important?
It tells us how many vectors we need to describe every vector in that space.
Exactly! For example, in 3D space, we need three vectors to form a basis. Remember, the concept of dimension also helps in understanding changes in our space, such as transformations. Let’s summarize what we’ve learned about vector spaces, subspaces, bases, and dimensions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Vector spaces are defined as sets of vectors that adhere to certain operations, while subspaces are subsets of these vector spaces that also maintain the properties of a vector space. The concepts of basis and dimension are crucial for understanding the structure of vector spaces.
Detailed
Vector Spaces and Subspaces
In linear algebra, a vector space is defined as a set of vectors that satisfies specific properties under two operations: vector addition and scalar multiplication. The foundational properties that characterize a vector space include closure, associativity, the existence of an additive identity, and the existence of additive inverses.
A subspace, on the other hand, is a subset of a vector space that retains the structure of a vector space under the same operations. For any subset to qualify as a subspace, it must itself satisfy the conditions that define a vector space. This leads to the important concepts of basis and dimension:
- Basis: A basis of a vector space is a set of linearly independent vectors that spans the entire space. Each vector in the vector space can be expressed as a linear combination of the basis vectors.
- Dimension: The dimension of a vector space is the number of vectors in a basis for that space, which signifies the degree of freedom within the space. Thus, the concepts of basis and dimension are critical for exploring the structure and behavior of vector spaces, as they provide insight into how many vectors are necessary to describe every element of the space.
Youtube Videos
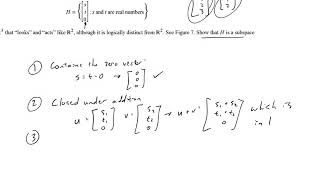
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Vector Space Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A set of vectors that satisfies the vector addition and scalar multiplication properties (closure, associativity, identity, inverse, distributivity).
Detailed Explanation
A vector space is a fundamental concept in linear algebra. It consists of a group of vectors that abide by certain rules for vector addition and scalar multiplication. To belong to a vector space, a set of vectors must follow five key properties: closure (adding two vectors in the set results in another vector in the set), associativity (the way vectors are added doesn't affect the outcome), identity (there exists a zero vector in the space), inverse (each vector has a corresponding negative vector), and distributive laws (scaling and adding vectors is consistent).
Examples & Analogies
Imagine a classroom where students can collaborate. If each collaboration (vector addition) leads to a productive discussion (still within the confines of the group), and there’s a neutral student who contributes nothing (the zero vector), then the classroom dynamics reflect a vector space.
Subspace Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A subset of a vector space that is itself a vector space under the same operations.
Detailed Explanation
A subspace is essentially a smaller 'universe' within a larger vector space. For a subset of vectors to be a subspace, it must itself be closed under vector addition and scalar multiplication, adhering to the same properties as the overarching vector space. Simply put, if you take some vectors from a vector space and they still fulfill all those properties, they form a subspace.
Examples & Analogies
Think of a large library (the vector space) filled with books on various subjects. A section of this library dedicated solely to mathematics books represents a subspace. Still, all the properties that apply to the entire library (like having a catalog and easy access) also apply within this section.
Basis and Dimension
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Basis: A set of linearly independent vectors that span the space.
• Dimension: The number of vectors in a basis.
Detailed Explanation
In a vector space, a basis is a specific set of vectors that are linearly independent, meaning none of the vectors can be represented as a combination of others in the set. This basis can generate any other vector in that vector space through linear combinations. The dimension of a vector space is defined as the number of vectors in this basis. Essentially, it tells us the 'size' of the vector space in terms of degrees of freedom for constructing vectors.
Examples & Analogies
Consider a music band where each instrument plays a unique role (the basis). If you have three different instruments like a guitar, drums, and a keyboard, they collectively can create a variety of music (span the space). Thus, the band's dimension is three, as it is determined by the number of distinct instruments that contribute independently to the music.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Space: Defined as a set of vectors that satisfy specific properties.
-
Subspace: A subset of a vector space that meets all vector space properties.
-
Basis: The collection of linearly independent vectors spanning a space.
-
Dimension: The number of vectors in a basis that determines the space's complexity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The set of all 2-dimensional vectors in R^2 forms a vector space.
-
The set of all vectors in R^3 lying on the xy-plane is a subspace of R^3.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a vector space wide and grand, addition and scalar go hand in hand.
📖 Fascinating Stories
-
Imagine a magical garden (the vector space) where unique flowers (vectors) intermingle only if they follow the garden's rules (properties). If you take a seed (subspace) from the garden, it'll grow into a smaller patch (subspace) that still follows the same conditions.
🧠 Other Memory Gems
-
Remember 'VSB' for Vector Space Basics: Vectors, Subspace, Basis.
🎯 Super Acronyms
A way to recall the properties of a vector space is 'CAIE' - Closure, Associativity, Identity, Inverse.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Space
Definition:
A set of vectors that satisfies properties of vector addition and scalar multiplication.
-
Term: Subspace
Definition:
A subset of a vector space that is also a vector space under the same operations.
-
Term: Basis
Definition:
A set of linearly independent vectors that spans a vector space.
-
Term: Dimension
Definition:
The number of vectors in a basis for the vector space.