Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to SVD
Unlock Audio Lesson
Today, we're diving into Singular Value Decomposition, or SVD. First, can anyone tell me what they believe SVD is?
Isn't it a way to break down matrices?
Exactly! SVD allows us to decompose a matrix into three matrices – U, Σ, and V^T. Remember the acronym ‘USV’ for the decomposition!
What do U, Σ, and V represent?
Great question! U and V are orthogonal matrices, indicating the direction of transformations, while Σ is a diagonal matrix with the singular values.
Properties of Orthogonal Matrices
Unlock Audio Lesson
Now, let’s talk about the orthogonal matrices, U and V. Can anyone define what 'orthogonal' means in this context?
It means the columns are perpendicular to one another, right?
Exactly! This orthogonality is crucial because it preserves geometric properties, ensuring no loss of information during the transformation. Can someone remember a property of orthogonal matrices?
They have the property that U^T U = I?
Correct! And that’s what makes them so powerful in SVD.
Applications of SVD
Unlock Audio Lesson
Alright! Let’s shift gears and discuss applications of SVD. Where do you think SVD is useful?
I think it can help with data compression.
Absolutely! SVD is widely used in data compression techniques. Who can relate that to how it’s beneficial in engineering?
Maybe in reducing the size of models for simulations?
Exactly! Reduced-order models facilitate efficient simulations in structural analysis. Excellent work!
Understanding Singular Values
Unlock Audio Lesson
Finally, let’s discuss the singular values from the diagonal matrix Σ. Why are these values critical?
I think they help in understanding the matrix's structure?
Exactly! They help identify the significance of each dimension when we perform PCA. Higher singular values mean that dimension carries more information, right?
So we can use those to determine which features to keep?
Right again! Excellent connections!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
SVD expresses any real matrix A as a product of three matrices: U, Σ, and V^T, where U and V are orthogonal matrices and Σ is a diagonal matrix. This decomposition has significant applications in data compression, principal component analysis (PCA), and reduced-order models in structural analysis.
Detailed
Singular Value Decomposition (SVD)
Singular Value Decomposition (SVD) is a method of decomposing a real matrix into three distinct matrices, typically written as:
$$ A = U \Sigma V^T $$
Where:
- U is an orthogonal matrix containing the left singular vectors.
- Σ is a diagonal matrix with non-negative singular values along the diagonal.
- V^T is the transpose of an orthogonal matrix containing the right singular vectors.
Key Points:
- Orthogonal Matrices: Matrices U and V represent rotations and reflections in Euclidean space, providing important geometric properties for transformations.
- Diagonal Matrix: The matrix Σ contains singular values which represent the
Youtube Videos
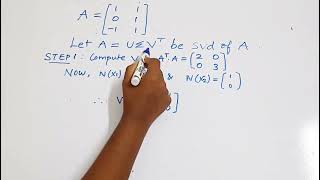
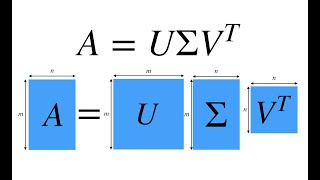
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of SVD
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For any real matrix A, SVD is:
$$A=UΣV^T$$
Where:
• U and V are orthogonal matrices.
• Σ is a diagonal matrix with singular values.
Detailed Explanation
Singular Value Decomposition, or SVD, is a method in linear algebra that decomposes a matrix into three other matrices. In the equation, 'A' represents any real matrix you start with. The matrix 'U' contains what are called 'left singular vectors', and 'V' contains 'right singular vectors'. Both 'U' and 'V' are orthogonal matrices, meaning their columns are orthogonal unit vectors. The diagonal matrix 'Σ' contains the singular values, which are the square roots of the eigenvalues of the matrix A multiplied by its transpose (A^T A). This decomposition helps understand the properties and structure of the matrix A.
Examples & Analogies
Imagine you have a complex, multi-layered cake (this is your matrix A) and you want to simplify it to understand its flavors better. By applying SVD, you separate the cake into distinct layers of flavors (the matrices U and V) and a concentrated syrup of sweetness (the singular values in Σ), making it easier to analyze and taste. Each component represents a different aspect of the original cake.
Applications of SVD
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications
• Data compression.
• Principal Component Analysis (PCA).
• Structural analysis using reduced-order models.
Detailed Explanation
SVD is a powerful tool widely used in various fields. One significant application is in data compression, where large datasets can be approximated using fewer dimensions, retaining most of the important information while reducing storage requirements. In Principal Component Analysis (PCA), SVD helps identify the directions (principal components) that capture the most variance in high-dimensional data. This is essential in machine learning and statistics for reducing dimensionality. Additionally, in structural engineering, SVD is utilized in reduced-order models to simplify complex structural behavior into manageable calculations, helping analyze structures efficiently.
Examples & Analogies
Think about when you take photographs on your phone. The original image file may be very large and take up a lot of space. To save room, your phone can compress the image using techniques similar to SVD, reducing the file size while keeping a version that's good enough to see clearly. Whether it's for making room on your device or simplifying the analysis of a bridge's design, SVD makes handling complex information easier and more efficient.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Singular Value Decomposition is a factorization technique for matrices.
-
Orthogonal matrices preserve angles and lengths, crucial in transformations.
-
Diagonal matrices contain singular values, representing the importance of corresponding dimensions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In Google’s PageRank algorithm, SVD is used to reduce the dimensions of data while preserving important characteristics.
-
In image compression, SVD helps retain essential features while discarding less important details, thus minimizing file size.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To break a matrix down, here’s the key, U, Σ, V, just follow me!
📖 Fascinating Stories
-
Imagine a magician, U, who twists and turns objects, Σ representing the strength, and V is the audience's view, all joined together to create a new spectacle.
🧠 Other Memory Gems
-
Remember ‘USV’ for using SVD—U for one orthogonal matrix, S for singular values, and V for the other orthogonal matrix.
🎯 Super Acronyms
SVD
- Singular Values Decomposition—think of it as breaking down the essential parts of a matrix.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Singular Value Decomposition (SVD)
Definition:
A technique to factorize a matrix into the product of three matrices: U, Σ, and V^T.
-
Term: Orthogonal Matrix
Definition:
A square matrix whose rows and columns are orthogonal unit vectors.
-
Term: Diagonal Matrix
Definition:
A matrix where all entries outside the main diagonal are zero.
-
Term: Singular Values
Definition:
Non-negative values that indicate the magnitude of each dimension in a matrix after SVD.