Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Orthogonal Vectors
Unlock Audio Lesson
Let's begin by defining orthogonal vectors. Two vectors are orthogonal if their dot product is zero. Can anyone explain what this means in terms of geometry?
It means that the vectors are at right angles to each other, like the axes on a graph.
Exactly! This is crucial when working with vector spaces because it ensures that vectors do not overlap in direction. Now, what is an orthonormal set?
An orthonormal set has vectors that are both orthogonal and have a length of one.
Correct! Remembering that an orthonormal set simplifies computations significantly because of the properties of unit vectors. Let’s take note of that. Any questions so far?
Can you give an example of where orthogonal vectors are used?
Good question! Orthogonal vectors are used in simplifications in various numerical methods, especially in solving linear systems. They help avoid errors in calculations. Let’s summarize the notion of orthogonality. First, orthogonal means zero dot product and implies independence. Second, orthonormal is orthogonal plus unit length.
Exploring the Gram-Schmidt Process
Unlock Audio Lesson
Next, we will discuss the Gram-Schmidt process. Can someone recall what this method accomplishes?
It converts a set of linearly independent vectors into an orthonormal set.
Exactly! The process helps ensure that numerical computations are stable. Let's talk about how it works. When given vectors, we begin with the first vector and normalize it. What does it mean to normalize a vector?
It means making its length equal to one.
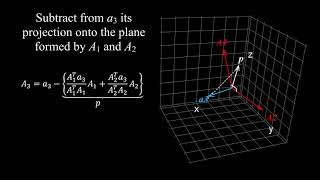
Right! After normalizing the first vector, you project the next vector onto the first and subtract that projection to maintain orthogonality. Does anyone remember the formula for projection?
It’s the dot product of the vector divided by the squared length of the base vector, multiplied by the base vector itself.
Perfect! Finally, we repeat the process with all the vectors. To sum up, the Gram-Schmidt process allows us to turn our vector set into an orthonormal basis which is essential in many applications, especially in numerical methods in engineering.
Applications of Orthonormal Sets
Unlock Audio Lesson
Now that we understand orthogonality and the Gram-Schmidt process, let’s explore their applications. Can anybody provide some context where these concepts might be applied realistically?
In structural engineering, where we need to analyze forces and stability?
Yes! The stability analysis often utilizes orthogonal components to simplify calculations. How about numerical methods?
For solving partial differential equations, they help ensure accurate solutions.
Great insights! The reliability of calculations in these methods is often linked to having an orthonormal basis, which reduces numerical error. Let’s conclude our discussion by reiterating the importance of both the concepts we focused on today and their significance in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we learn about orthogonality, which defines when two vectors are orthogonal (their dot product is zero). Additionally, the Gram-Schmidt process is detailed as a systematic way to convert a set of linearly independent vectors into an orthonormal set, with implications for numerical applications in engineering.
Detailed
Orthogonality and Gram-Schmidt Process
Orthogonal Vectors
Two vectors u and v are orthogonal if their dot product is zero, symbolically represented as:
table{u v = 0}
This relationship highlights that when two vectors are orthogonal, they are at right angles to each other in a geometric sense, which is crucial in various applications, particularly in the context of vector spaces where independence is required.
Orthonormal Set
An orthonormal set consists of vectors that are both orthogonal and unit vectors (having a magnitude of 1). Each vector contributes uniquely to the direction in the vector space while maintaining unit distance.
Gram-Schmidt Process
The Gram-Schmidt process provides a method for taking a set of linearly independent vectors and transforming them into an orthonormal basis. This process is especially significant in numerical linear algebra where maintaining numerical stability is essential.
Applications
The Gram-Schmidt process is utilized in various numerical methods, such as the finite element method in structural analysis and solving partial differential equations. The implementation of orthonormality enhances the robustness and accuracy of these methods, which are fundamental in modern engineering practices.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Orthogonal Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Two vectors u and v are orthogonal if:
$$u·v = 0$$
Detailed Explanation
Orthogonal vectors are vectors that are at right angles to each other. Mathematically, this means that the dot product of the two vectors equals zero. The dot product measures how much one vector extends in the direction of another. If the dot product is zero, the vectors are perpendicular, indicating that there is no component of one vector in the direction of the other.
Examples & Analogies
Think of two roads that intersect at a right angle. One road represents vector u, and the other road represents vector v. These roads are 'orthogonal' because they meet at a 90-degree angle, showing no overlap in direction.
Orthonormal Set
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A set of vectors that are both orthogonal and unit vectors.
Detailed Explanation
An orthonormal set is a collection of vectors that not only are orthogonal to each other but also each have a length (or magnitude) of one. This property is important in various mathematical applications as it simplifies calculations, especially in terms of length and angles. Each vector being a unit vector means that the dot product of any two different vectors in the set is zero, while the dot product of any vector with itself is one.
Examples & Analogies
Imagine a set of arrows placed in a 3D space, pointing north, east, and up. Each arrow is distinct (orthogonal), and they all have the same length of one meter (unit vectors). This scenario describes an orthonormal set of vectors where the directions are easily distinguishable and comparable.
Gram-Schmidt Process
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A method to convert a set of linearly independent vectors into an orthonormal set.
Detailed Explanation
The Gram-Schmidt Process is a systematic method used in linear algebra to take a set of linearly independent vectors and transform them into an orthonormal set. This process involves taking one vector at a time, modifying it to ensure orthogonality with the previously selected vectors, and then normalizing each vector to ensure they have a unit length. It is a crucial technique for simplifying many complex equations and calculations in vector spaces.
Examples & Analogies
Think of a group of friends who want to line up in a way that they are evenly spaced and facing different directions. The Gram-Schmidt Process would be like giving each friend specific instructions to ensure they stand at right angles to each other (orthogonality) and take one step back (normalizing their positions) so they don't crowd each other but remain visually distinct. By following these instructions, they create an ideal display of their unique positions without overlapping.
Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications include:
- Numerical solutions of partial differential equations.
- Finite element methods in structural analysis.
Detailed Explanation
The processes of orthogonality and the Gram-Schmidt method are crucial in various fields of engineering and applied mathematics. For instance, in solving partial differential equations, having an orthonormal basis simplifies the computational tasks, making numerical methods more efficient and accurate. Additionally, in structural analysis, the finite element method relies on these concepts to ensure the stability and accuracy of dynamic simulations.
Examples & Analogies
Imagine you are building a complex bridge. To predict how it will behave under various forces, engineers use models made up of small, manageable pieces (finite elements). Each small piece (vector) needs to be at the right angle to represent its independent behavior accurately. Just like how a game board allows pieces to fit together without overlap, using orthonormal sets allows accurate representation without complications during simulations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonal Vectors: Vectors with a dot product of zero, indicating they are perpendicular to one another.
-
Orthonormal Set: A type of vector set that is both orthogonal and consists of unit vectors.
-
Gram-Schmidt Process: Algorithm for converting linearly independent vectors into an orthonormal set.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In 3D space, the vectors (1, 0, 0) and (0, 1, 0) are orthogonal since their dot product is 0.
-
Applying the Gram-Schmidt process to the vectors (1, 1, 0) and (1, 0, 1) can yield an orthonormal set.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Ortho and normal, a perfect pair, at right angles they stand, with unity in their flair.
📖 Fascinating Stories
-
Imagine a city where every vector wants to be unique. The Gram-Schmidt process sends out invites to parties. Each vector arrives. The first gets normalized to fit in, while others learn to align orthogonally, ensuring they all stand out as friends, not foes.
🧠 Other Memory Gems
-
For orthogonality, remember O-N: O for Orthogonal, N for Normal (unit length).
🎯 Super Acronyms
OG - Orthogonal & Gram-Schmidt (the heroes of numerical methods).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonal Vectors
Definition:
Two vectors are orthogonal if their dot product is zero, indicating they are at right angles to each other.
-
Term: Orthonormal Set
Definition:
A set of vectors that are both orthogonal and unit vectors, simplifying many calculations.
-
Term: GramSchmidt Process
Definition:
A method for converting a set of linearly independent vectors into an orthonormal set.