Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Transpose
Unlock Audio Lesson
Today, we'll dive into the concept of transposing a matrix. Can anyone tell me what they think happens when we transpose a matrix?
I think we're just rearranging the numbers somehow?
Exactly! When we transpose a matrix, we swap its rows and columns. For example, if we have a matrix A, its transpose is represented as A^T.
So, if A is a 2x3 matrix, what would A^T be like?
Great question! A 2x3 matrix has 2 rows and 3 columns, so its transpose A^T would be a 3x2 matrix. Each element will switch its position accordingly.
And does that affect the way we calculate things with matrices?
Absolutely! The transpose operation has implications for matrix addition, multiplication, and more. Remember, the operation is simple but powerful!
Properties of Transpose
Unlock Audio Lesson
Now let's look at some properties of transposes. Can anyone tell me what happens if we take the transpose of the transpose? Any guesses?
Wouldn't it just go back to the original matrix?
Correct! We have the property, $$(A^T)^T = A$$. This shows that transposing a matrix twice brings it back to its original form.
What about adding two matrices together? Does that change anything?
Good point! The transpose of the sum of two matrices equals the sum of their transposes: $$(A + B)^T = A^T + B^T$$.
Does it also work for multiplication?
Exactly! The product of two matrices transposed is the reverse product of their transposes: $$(AB)^T = B^T A^T$$.
These properties seem really useful!
They are! Understanding these can simplify many calculations in linear algebra.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the transpose of a matrix is defined as the operation where rows become columns and columns become rows. This operation has unique properties that play a crucial role in various applications, particularly in solving systems of equations and understanding matrix operations.
Detailed
Transpose of a Matrix
The transpose of a matrix is a crucial concept in linear algebra that involves reorienting a matrix by swapping its rows with its columns. If we denote the transpose of a matrix A as A^T, it is defined mathematically such that the element in the i-th row and j-th column of A becomes the element in the j-th row and i-th column of A^T. This simple yet powerful operation has significant implications for various mathematical computations and applications.
Key Properties of Transposes
- Double Transpose: The transpose of a transpose returns the original matrix:
$$(A^T)^T = A$$ - Sum of Matrices: The transpose of a sum is equal to the sum of transposes:
$$ (A + B)^T = A^T + B^T $$ - Product of Matrices: The transpose of a product of matrices is equal to the product of their transposes in reverse order:
$$ (AB)^T = B^T A^T $$
These properties illustrate the inherent symmetry in matrix operations and underpin many advanced mathematical techniques such as solving linear equations and eigenvalue problems.
Youtube Videos
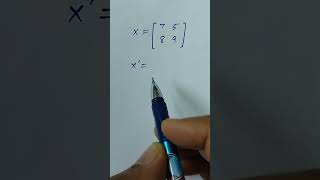
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Transpose
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Rows become columns.
• (AT)T =A
Detailed Explanation
The transpose of a matrix is formed by turning its rows into columns. For instance, if you have a matrix represented as a table, the first row of numbers will become the first column in the new table. The notation (AT)T = A indicates that if you take the transpose of a transposed matrix, you will return to the original matrix.
Examples & Analogies
Think of transposing a matrix as flipping a photo on its side; what was previously horizontal is now vertical. Just like flipping a picture back over returns it to its original state, applying the transpose operation twice brings you back to the starting matrix.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Transpose: The operation where rows of a matrix become columns and vice versa.
-
Properties of Transpose: Includes $(A^T)^T = A$, $(A + B)^T = A^T + B^T$, and $(AB)^T = B^T A^T.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If A = [[1, 2, 3], [4, 5, 6]], then A^T = [[1, 4], [2, 5], [3, 6]].
-
For a 3x2 matrix B = [[7, 8], [9, 10], [11, 12]], the transpose B^T = [[7, 9, 11], [8, 10, 12]].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Transpose, rows to columns it does flow, watch the numbers move to and fro!
📖 Fascinating Stories
-
Imagine a movie set where actors switch roles; that's how the transpose makes rows change into columns!
🧠 Other Memory Gems
-
To remember transposes, remember: 'Rotate R-C' for Row to Column change.
🎯 Super Acronyms
T-R-C
- Transpose means Rows change to Columns.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Transpose
Definition:
The operation of swapping the rows and columns of a matrix.
-
Term: Matrix Product
Definition:
The result of multiplying two matrices.
-
Term: Matrix Sum
Definition:
The result of adding two matrices of the same dimensions.